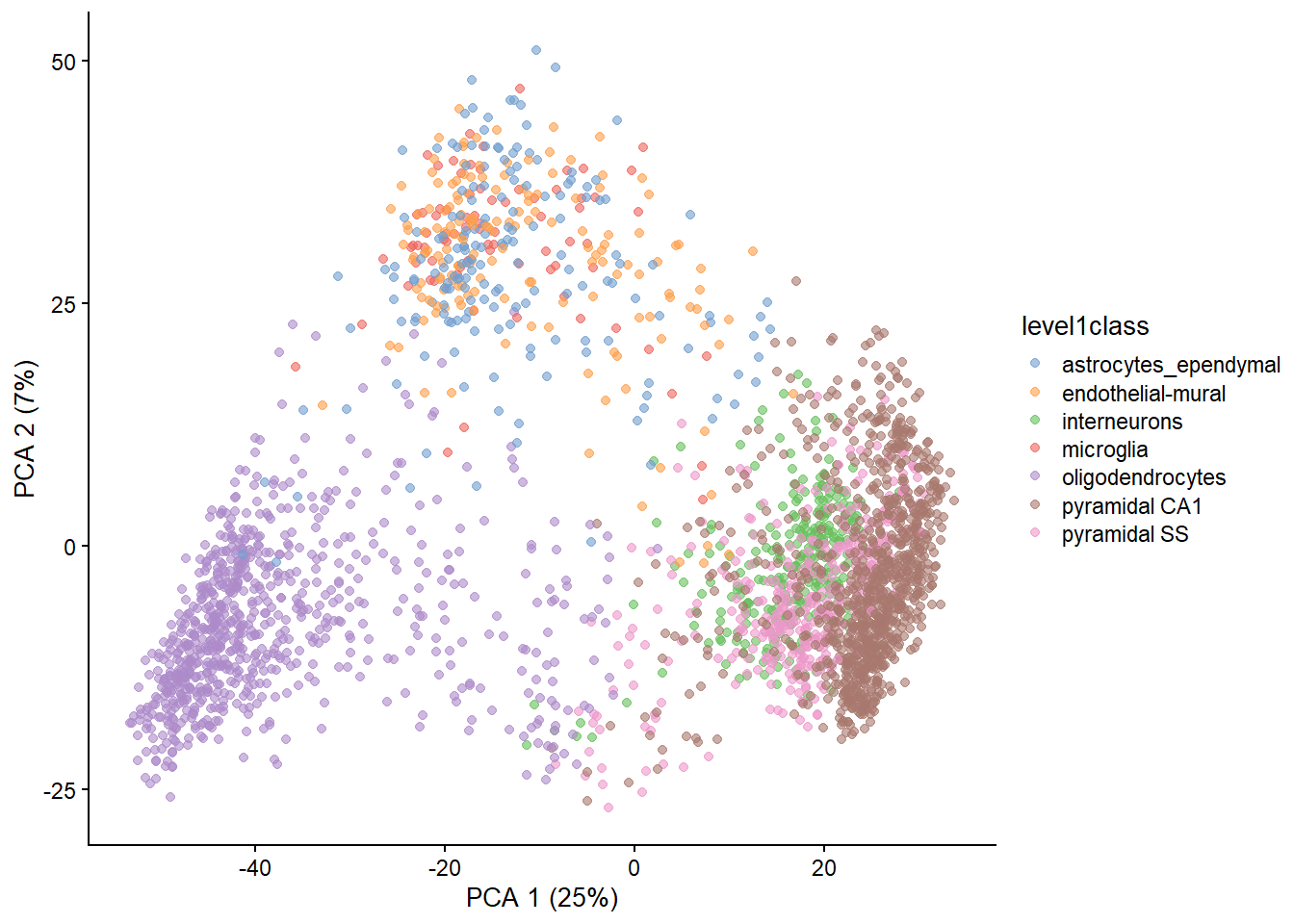
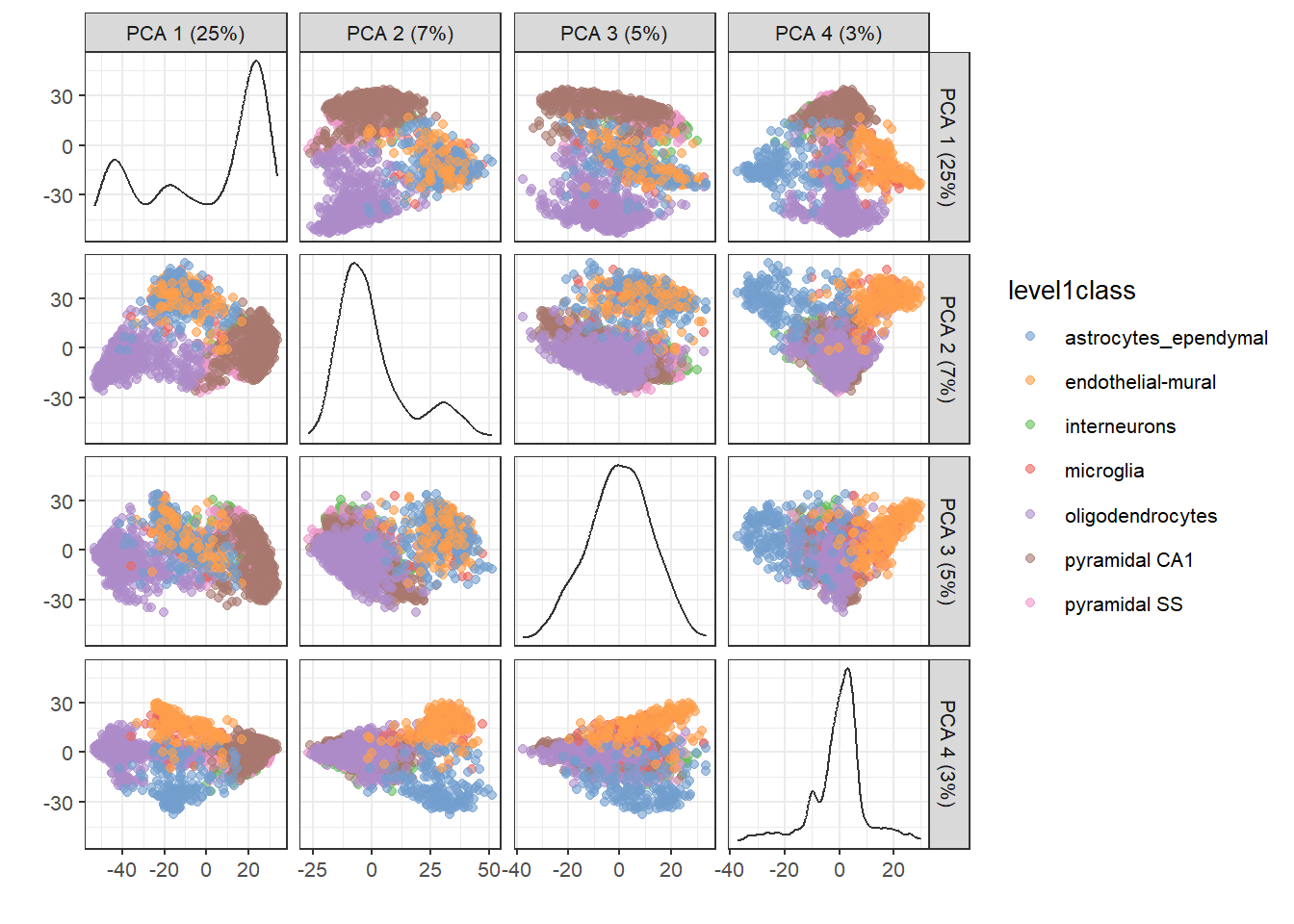
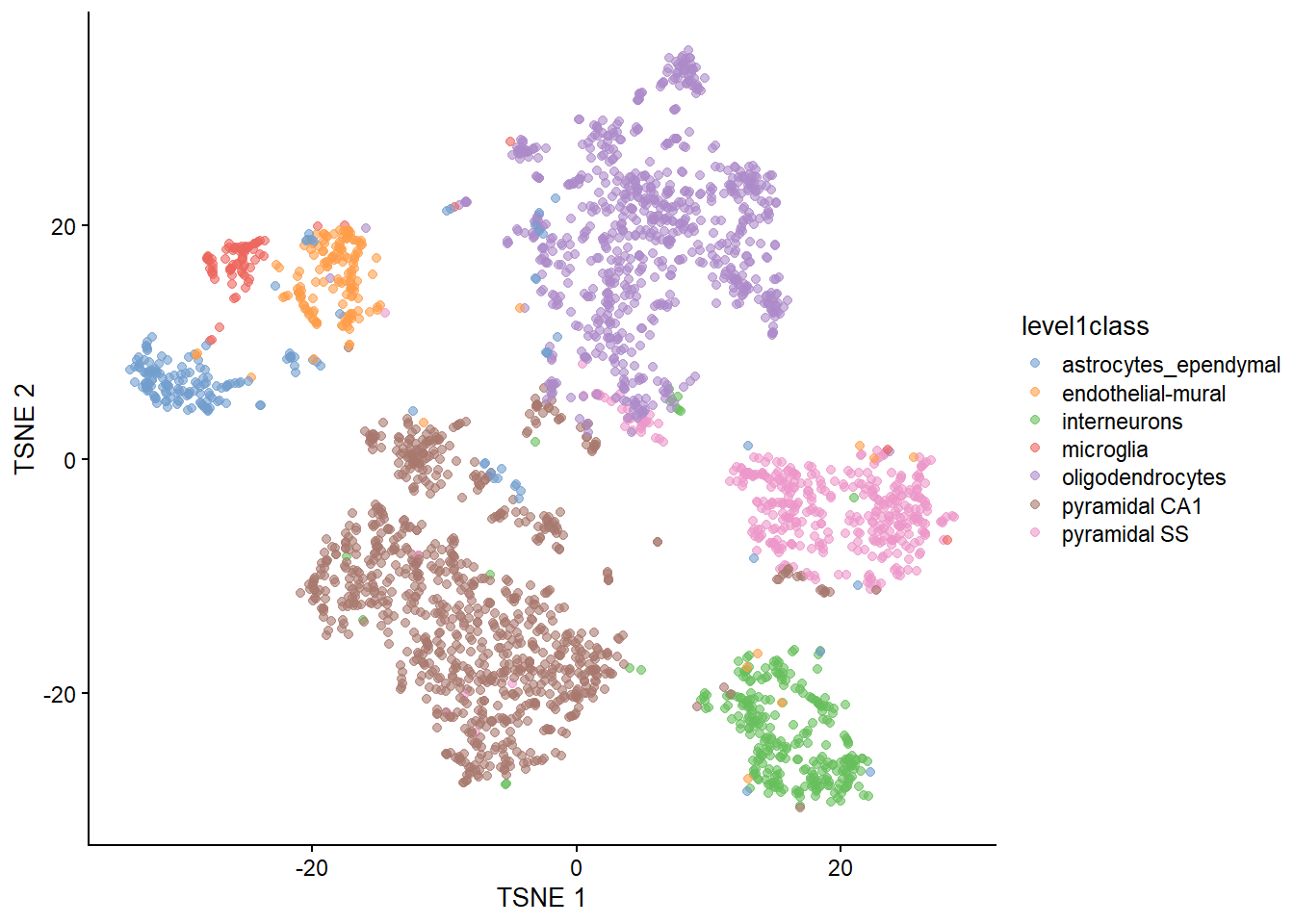
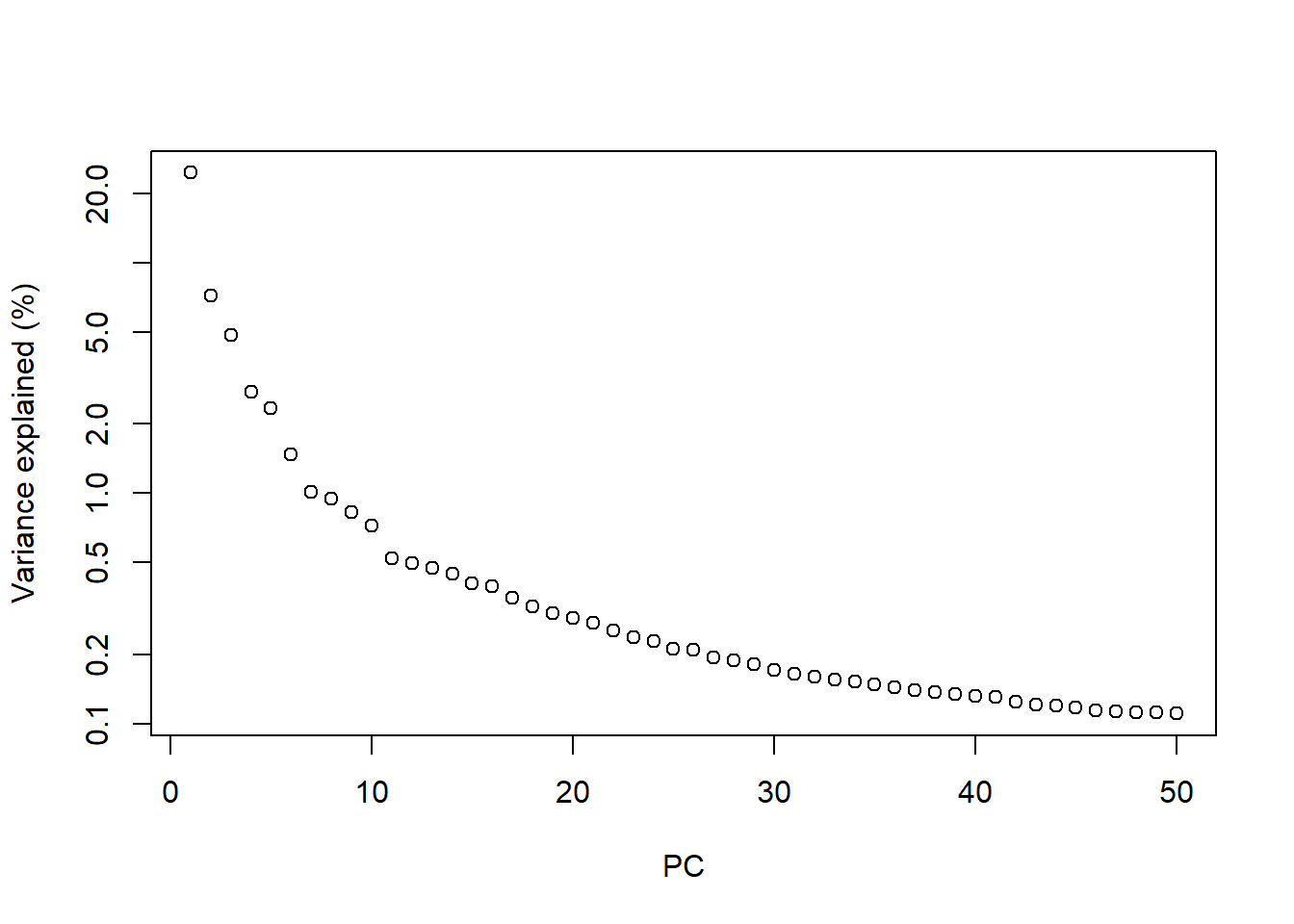```{r} #| include: false conflicts_prefer(GenomicRanges::setdiff) ``` # 降维 ```{r loading-ZeiselBrainData} #--- loading ---# library(scRNAseq) sce.zeisel <- ZeiselBrainData() library(scater) sce.zeisel <- aggregateAcrossFeatures(sce.zeisel, id=sub("_loc[0-9]+$", "", rownames(sce.zeisel))) #--- gene-annotation ---# library(org.Mm.eg.db) rowData(sce.zeisel)$Ensembl <- mapIds(org.Mm.eg.db, keys=rownames(sce.zeisel), keytype="SYMBOL", column="ENSEMBL") #--- quality-control ---# stats <- perCellQCMetrics(sce.zeisel, subsets=list( Mt=rowData(sce.zeisel)$featureType=="mito")) qc <- quickPerCellQC(stats, percent_subsets=c("altexps_ERCC_percent", "subsets_Mt_percent")) sce.zeisel <- sce.zeisel[,!qc$discard] #--- normalization ---# library(scran) set.seed(1000) clusters <- quickCluster(sce.zeisel) sce.zeisel <- computeSumFactors(sce.zeisel, cluster=clusters) sce.zeisel <- logNormCounts(sce.zeisel) #--- variance-modelling ---# dec.zeisel <- modelGeneVarWithSpikes(sce.zeisel, "ERCC") top.hvgs <- getTopHVGs(dec.zeisel, prop=0.1) ``` ```{r} ``` ## 主成分分析 ```{r} library (scran)<- getTopHVGs (dec.zeisel, n= 2000 )set.seed (100 ) # See below. <- fixedPCA (sce.zeisel, subset.row= top.zeisel) # 默认情况下,将计算前 50 个 PC reducedDimNames (sce.zeisel)``` ```{r} dim (reducedDim (sce.zeisel, "PCA" ))``` `set.seed()` 获得可重复的结果。```{r} library (BiocSingular)set.seed (1000 )<- fixedPCA (sce.zeisel, subset.row= top.zeisel, BSPARAM= RandomParam (), name= "randomized" )reducedDimNames (sce.zeisel)``` ```{r} dim (reducedDim (sce.zeisel, "randomized" ))``` ### 选择主成分数量 ```{r} <- attr (reducedDim (sce.zeisel), "percentVar" )plot (percent.var, log= "y" , xlab= "PC" , ylab= "Variance explained (%)" )``` ### 可视化主成分 ```{r} library (scater)plotReducedDim (sce.zeisel, dimred= "PCA" , colour_by= "level1class" )``` ```{r} plotReducedDim (sce.zeisel, dimred= "PCA" , ncomponents= 4 ,colour_by= "level1class" )``` ## t-分布随机邻域嵌入 [ t-stochastic neighbor embedding (t-SNE) ](https://jmlr.csail.mit.edu/beta/papers/v9/vandermaaten08a.html) 是一种非线性降维方法。它试图寻找数据的低维表示,其保留了每个点与其相邻点在高维空间中的距离。t-SNE 在低维空间中排列细胞的方式具有更大的自由度,使其能够在复杂的群体中分离许多不同的簇。`runTSNE()` 中设置`dimred="PCA"` 使得t-SNE在 top PCs 中计算。这利用了PCA的数据压缩和噪声去除,以获得更快、更整洁的结果。[ t-SNE 超参数 ](https://distill.pub/2016/misread-tsne/) 1. 困惑度perplexity(5 - 50)2. 学习率epsilon3. 迭代次数 step```{r} #| label: fig-tsne set.seed (00101001101 )# runTSNE() stores the t-SNE coordinates in the reducedDims # for re-use across multiple plotReducedDim() calls. <- runTSNE (sce.zeisel, dimred= "PCA" )reducedDimNames (sce.zeisel)plotReducedDim (sce.zeisel, dimred= "TSNE" , colour_by= "level1class" )``` ```{r} set.seed (100 )<- runTSNE (sce.zeisel, dimred= "PCA" , perplexity= 5 )<- plotReducedDim (sce.zeisel, dimred= "TSNE" ,colour_by= "level1class" ) + ggtitle ("perplexity = 5" )set.seed (100 )<- runTSNE (sce.zeisel, dimred= "PCA" , perplexity= 20 )<- plotReducedDim (sce.zeisel, dimred= "TSNE" ,colour_by= "level1class" ) + ggtitle ("perplexity = 20" )set.seed (100 )<- runTSNE (sce.zeisel, dimred= "PCA" , perplexity= 80 )<- plotReducedDim (sce.zeisel, dimred= "TSNE" , colour_by= "level1class" ) + ggtitle ("perplexity = 80" ):: grid.arrange (out5, out20, out80, ncol= 3 )``` ## 均匀流形近似和投影 [ Uniform manifold approximation and projection(UMAP) ](https://arxiv.org/abs/1802.03426) 也是一种非线性降维方法。UMAP 是可视化大型scRNA-seq数据集的首选方法。[ umap 超参数 ](https://umap-learn.readthedocs.io/en/latest/parameters.html) 1. n_neighbors 局部结构-全局结构权衡2. min_dist 紧密程度3. n_components 降维空间的维数4. metric 距离的计算方式```{r} #| label: fig-umap set.seed (1100101001 )<- runUMAP (sce.zeisel, dimred= "PCA" )plotReducedDim (sce.zeisel, dimred= "UMAP" , colour_by= "level1class" )```