7  方差分析

Modified

November 20, 2024

方差分析的假设

  1. 独立性

  2. 正态性 shapiro.test()

  3. 方差齐性 正态 bartlett.test()，非正态Levene's test

7.1 单因素组间方差分析

7.1.1 计算公式

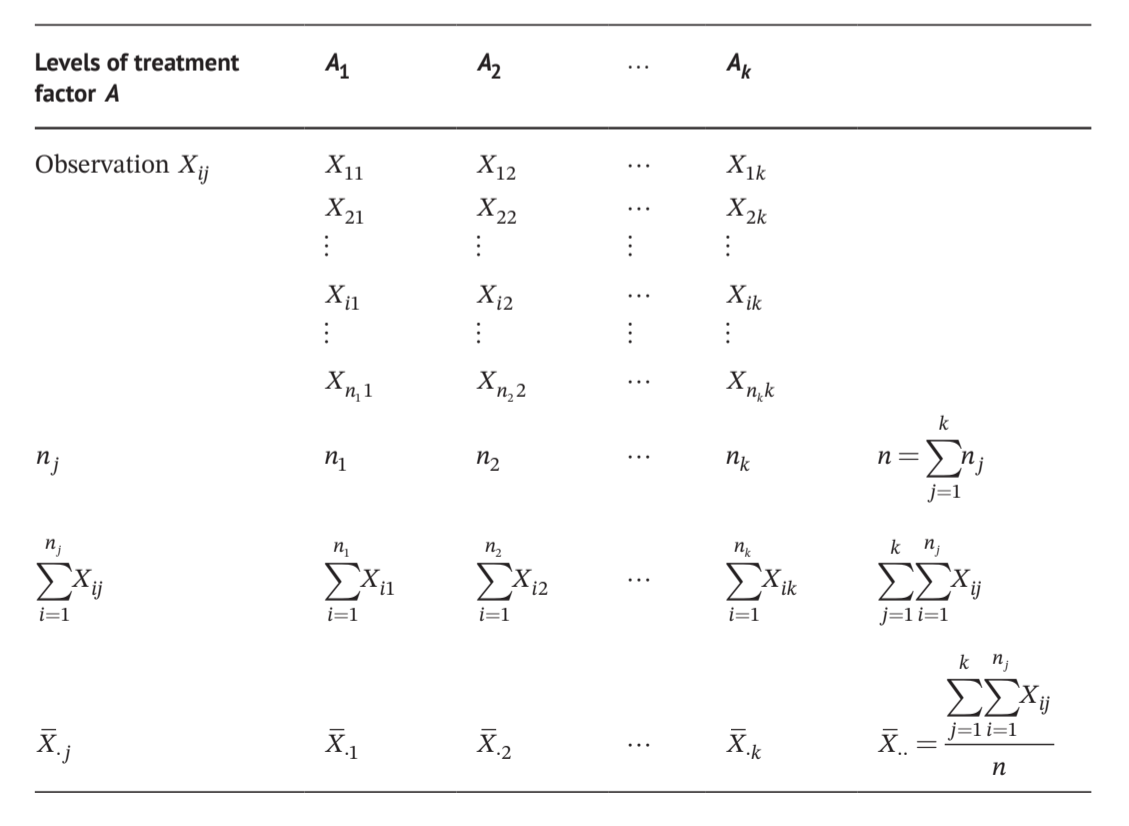
因子A有\(A_1,A_2,...,A_k\)共k个水平

total sum of squares

\[ SS_T=\sum_{j=1}^{k}\sum_{i=1}^{n_j}X_{ij}^2-\frac{(\sum_{j=1}^{k}\sum_{i=1}^{n_j}X_{ij})^2}{n}=SS_{组间}+SS_{组内} \]

between groups sum of squares \[ SS_{组间}=\sum_{j=1}^{k}\frac{(\sum_{i=1}^{n_j}X_{ij})^2}{n_j}-\frac{(\sum_{j=1}^{k}\sum_{i=1}^{n_j}X_{ij})^2}{n} \]

自由度\(\nu=n-1,\nu_{组间}=k-1,\nu_{组内}=\sum_{j=1}^{k}(n_j-1)=n-k\)

Between groups mean square \(MS_{组间}=\frac{SS_{组间}}{k-1}\)

Within groups mean square \(MS_{组内}=\frac{SS_{组内}}{n-k}\)

\[H_0:\mu_1=\mu_2=...=\mu_k\]

\[ \frac{SS_T}{\sigma^2}\sim \chi^2(\nu),\nu=n-1 \] \[ \frac{SS_{组内}}{\sigma^2}\sim \chi^2(\nu),\nu=n-k \] 因此，

\[ \frac{SS_{组间}}{\sigma^2}=\frac{SS_T}{\sigma^2}-\frac{SS_{组内}}{\sigma^2}\ \ \ \sim \chi^2(\nu),\nu=k-1 \]

检验统计量

\[ F=\frac{\frac{SS_{组间}}{(k-1)\sigma^2}}{\frac{SS_{组内}}{(n-k)\sigma^2}}=\frac{\frac{SS_{组间}}{k-1}}{\frac{SS_{组内}}{n-k}}=\frac{MS_{组间}}{MS_{组内}}\ \ \ \sim \chi^2(\nu),\nu=k-1 \]

Show the code
df <- tibble(
    low=c(53.5,43.7,46.5,50.3,56.1),
    medium=c(33.2,30.6,23.9,26.4,35.9),
    high=c(11.5,21.9,18.6,13.6,9.5)
)

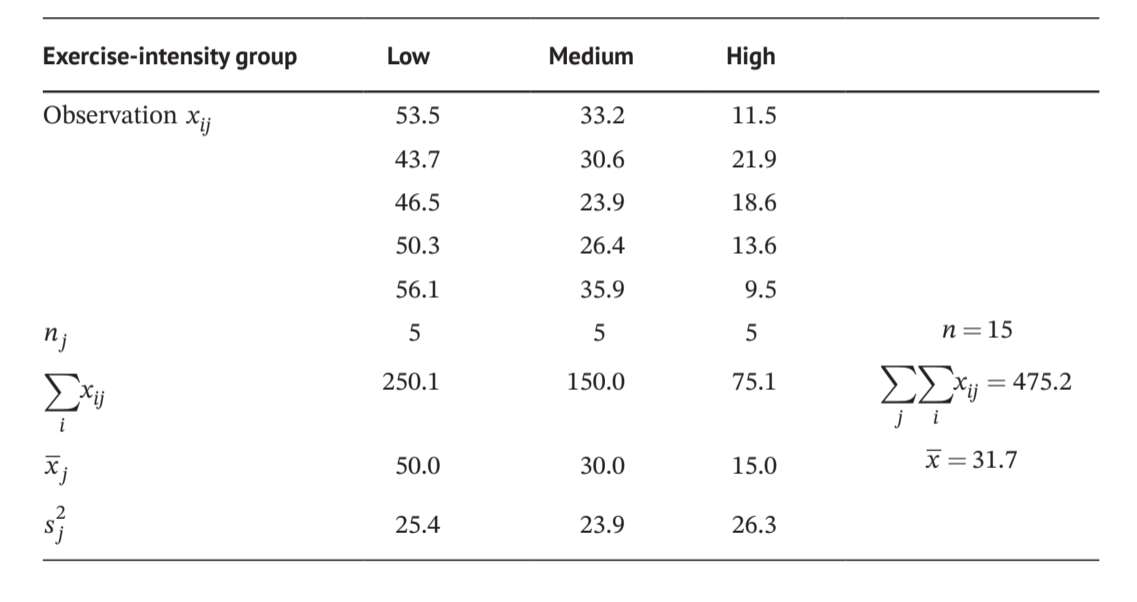
7.1.2 手算

Show the code
k <- 3
df_sum <- sum(df)
df_sum_square <- sum(df^2)
n <- 15
C <- df_sum^2/n

SS_T <- df_sum_square-C
SS_between <- apply(df, 2, function(x) sum(sum(x)^2/length(x))) |> sum()-C

SS_within <- SS_T-SS_between

MS_between <- SS_between/(k-1)
MS_within <- SS_within/(n-k)
F_stat <-MS_between/MS_within 

p_value <- pf(F_stat,2,12,lower.tail = F)

7.1.3 stats::aov()

Show the code
df_long <- df |> pivot_longer(cols = everything(),
                              names_to = "level",
                              values_to = "value")
df_long$level <- factor(df_long$level)
df_aov <- aov(value~level,data = df_long)

anova(df_aov)
#> Analysis of Variance Table
#> 
#> Response: value
#>           Df Sum Sq Mean Sq F value    Pr(>F)    
#> level      2 3083.7 1541.83  61.245 5.046e-07 ***
#> Residuals 12  302.1   25.17                      
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

7.1.4 ez::ezANOVA()

Show the code
df_long <- df_long |> rowid_to_column(var = "id") |> 
    relocate(id,.before = 1) |> mutate(id=factor(id))

ez::ezANOVA(data = df_long,
            dv = value,
            wid = id,
            between = level,
            type = 3,
            detailed = T)
#> $ANOVA
#>        Effect DFn DFd       SSn     SSd         F            p p<.05       ges
#> 1 (Intercept)   1  12 15054.336 302.096 597.99545 1.318663e-11     * 0.9803277
#> 2       level   2  12  3083.668 302.096  61.24546 5.045797e-07     * 0.9107746
#> 
#> $`Levene's Test for Homogeneity of Variance`
#>   DFn DFd        SSn   SSd           F         p p<.05
#> 1   2  12 0.05733333 92.36 0.003724556 0.9962835

7.1.5 stats::lm()

Show the code
lm_aov <- lm(formula = value ~  level, data = df_long)
lm_aov
#> 
#> Call:
#> lm(formula = value ~ level, data = df_long)
#> 
#> Coefficients:
#> (Intercept)     levellow  levelmedium  
#>       15.02        35.00        14.98

anova(lm_aov)
#> Analysis of Variance Table
#> 
#> Response: value
#>           Df Sum Sq Mean Sq F value    Pr(>F)    
#> level      2 3083.7 1541.83  61.245 5.046e-07 ***
#> Residuals 12  302.1   25.17                      
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

model.matrix(~ level, data = df_long)
#>    (Intercept) levellow levelmedium
#> 1            1        1           0
#> 2            1        0           1
#> 3            1        0           0
#> 4            1        1           0
#> 5            1        0           1
#> 6            1        0           0
#> 7            1        1           0
#> 8            1        0           1
#> 9            1        0           0
#> 10           1        1           0
#> 11           1        0           1
#> 12           1        0           0
#> 13           1        1           0
#> 14           1        0           1
#> 15           1        0           0
#> attr(,"assign")
#> [1] 0 1 1
#> attr(,"contrasts")
#> attr(,"contrasts")$level
#> [1] "contr.treatment"
lm(formula = value ~ 0 + level, data = df_long)
#> 
#> Call:
#> lm(formula = value ~ 0 + level, data = df_long)
#> 
#> Coefficients:
#>   levelhigh     levellow  levelmedium  
#>       15.02        50.02        30.00
model.matrix(~ 0 + level, data = df_long)
#>    levelhigh levellow levelmedium
#> 1          0        1           0
#> 2          0        0           1
#> 3          1        0           0
#> 4          0        1           0
#> 5          0        0           1
#> 6          1        0           0
#> 7          0        1           0
#> 8          0        0           1
#> 9          1        0           0
#> 10         0        1           0
#> 11         0        0           1
#> 12         1        0           0
#> 13         0        1           0
#> 14         0        0           1
#> 15         1        0           0
#> attr(,"assign")
#> [1] 1 1 1
#> attr(,"contrasts")
#> attr(,"contrasts")$level
#> [1] "contr.treatment"

7.1.6 事后检验

成对比较的数量 \(N=\frac{k!}{2!(k-2)!},k≥3\)，导致犯第Ⅰ类错误的概率迅速增加，\([1-(1-\alpha)^N]\)。

7.1.6.1 Tukey’s test

Tukey’s test 也被称为Tukey’s honestly significant difference (Tukey’s HSD) test。

  1. k个均值从大到小排列；
  2. 均值最大的组依次与均值最小，第二小，……，第二大比较；
  3. 均值第二大的组以同样的方式比较；
  4. 以此类推
  5. 在各组样本量相等的情况下，如果在两个均值之间未发现显著差异，则推断这两个均值所包含的任何均值之间不存在显著差异，并且不再检验所包含均值之间的差异。

studentized range statistic \(q=\frac{\bar X_{max}-\bar X_{min}}{S_{\bar X_{max}-\bar X_{min}}}\)，其中\(S_{\bar X_{max}-\bar X_{min}}=\sqrt{\frac{MS_{组内}}{n}}\)，\(n\)是每一个治疗组的样本量。

如果各组样本量不等,则\(S_{\bar X_{max}-\bar X_{min}}=\sqrt{\frac{MS_{组内}}{2}(\frac{1}{n_i}+\frac{1}{n_j})}\)

检验统计量

\[ HSD=q_{(k,\nu_{组内}),1-\alpha} \times S_{\bar X_{max}-\bar X_{min}},\nu_{组内}=k(n_j-1) \]

对于任意i,j且\(\bar X_i＞\bar X_j\)，如果\(\bar X_i-\bar X_j＞HSD\)，那么拒绝\(H_0\)，说明这两组存在显著差异。

\[ H_0:\mu_i=\mu_j(i≠j) \]

Show the code
k_means <- apply(df,2,mean) |> sort(,decreasing = TRUE)
k_means
#>    low medium   high 
#>  50.02  30.00  15.02

# 附录q  q(3,12),1-0.05  3(5-1)=12
q_critical_value <- 3.77
nj <- 5
HSD <- q_critical_value*sqrt(MS_within/nj)

k_means
#>    low medium   high 
#>  50.02  30.00  15.02
diff_means <- c()
names_diff_means <- c()

for(i in 1:(length(k_means)-1)){
    for(j in length(k_means):(i+1)){
        diff_value <- k_means[i] - k_means[j]
        diff_means <- c(diff_means, diff_value)
        names_diff_means <- c(names_diff_means, paste(names(k_means)[i], "vs.", names(k_means)[j],sep = "_"))
    }
}
names(diff_means) <- names_diff_means
diff_means
#>    low_vs._high  low_vs._medium medium_vs._high 
#>           35.00           20.02           14.98
#全为真，3组成对比较都存在显著差异
diff_means > HSD 
#>    low_vs._high  low_vs._medium medium_vs._high 
#>            TRUE            TRUE            TRUE
Show the code
pairwise <- TukeyHSD(df_aov)
pairwise
#>   Tukey multiple comparisons of means
#>     95% family-wise confidence level
#> 
#> Fit: aov(formula = value ~ level, data = df_long)
#> 
#> $level
#>               diff        lwr       upr     p adj
#> low-high     35.00  26.534054  43.46595 0.0000003
#> medium-high  14.98   6.514054  23.44595 0.0013315
#> medium-low  -20.02 -28.485946 -11.55405 0.0001069

7.1.6.2 Dunnett’s test

Dunnett’s test也称为q’-test,是两独立样本t-test的一种修正。Dunnett’s test 假设数据符合正态分布，并且各组的方差相等。 控制对照组（C）与其他每个实验组（T）比较。

\(H_0:\mu_C=\mu_T\)

\[ q'=\frac{\bar X_T-\bar X_C}{\sqrt{MS_{组内}(\frac{1}{n_T}+\frac{1}{n_C})}} \sim q'(\nu,a) \ \ \nu=\nu_{组内},a=k \]

临界值 \(q'_{(a,\nu_E),1-\alpha/2}\)

Show the code
nT <- nC <- 5 

SE_mean_diff <- sqrt(MS_within*(1/nT+1/nC))

k_means
#>    low medium   high 
#>  50.02  30.00  15.02
diff_means <- c()
names_diff_means <- c()

# 以 low 作控制组
for(i in 2:length(k_means)){
        diff_value <- k_means[i] - k_means[1]
        diff_means <- c(diff_means, diff_value)
        names_diff_means <- c(names_diff_means, paste(names(k_means)[1], "vs.", names(k_means)[i],sep = "_"))
}
names(diff_means) <- names_diff_means
diff_means
#> low_vs._medium   low_vs._high 
#>         -20.02         -35.00

q撇_stat <- diff_means/SE_mean_diff

# 附录q'  q'(3,12),1-0.05/2  
abs(q撇_stat)>2.50  
#> low_vs._medium   low_vs._high 
#>           TRUE           TRUE
#全为真，各实验组与控制组均存在显著差异
Show the code
library(multcomp)
dunnett_result <- glht(df_aov, linfct =mcp(level =c("medium - low = 0", "high - low = 0")))

# 查看 Dunnett's test 结果
summary(dunnett_result)
#> 
#>   Simultaneous Tests for General Linear Hypotheses
#> 
#> Multiple Comparisons of Means: User-defined Contrasts
#> 
#> 
#> Fit: aov(formula = value ~ level, data = df_long)
#> 
#> Linear Hypotheses:
#>                   Estimate Std. Error t value Pr(>|t|)    
#> medium - low == 0  -20.020      3.173  -6.309 7.46e-05 ***
#> high - low == 0    -35.000      3.173 -11.030 2.38e-07 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> (Adjusted p values reported -- single-step method)

7.1.6.3 LSD-t test

least significant difference t-test

挑选任意感兴趣的两组进行比较

\[ H_0:\mu_i=\mu_j(i≠j) \]

\[ LSD-t=\frac{\bar X_i-\bar X_j}{\sqrt{MS_{组内}(\frac{1}{n_i}+\frac{1}{n_j})}} \sim t(\nu) \ ,\ \nu=\nu_{组内}=n-k,a=k \]

Show the code
# medium high
LSD <- (k_means[2]-k_means[3])/sqrt(MS_within*(1/5+1/5))

# 附录 t(12,1-0.05/2)=2.719

7.2 方差分析假设

https://www.statmethods.net/stats/rdiagnostics.html

7.2.1 独立性

7.2.2 正态性

Show the code
# 异常观测点

car::outlierTest(df_aov) 
#> No Studentized residuals with Bonferroni p < 0.05
#> Largest |rstudent|:
#>   rstudent unadjusted p-value Bonferroni p
#> 6  1.63682            0.12993           NA

7.2.2.1 直方图/茎叶图

7.2.2.2 P-P图/Q-Q图

7.2.2.3 偏度和峰度

\[ H_0:总体偏度系数\gamma_1=0 或者总体峰度系数\gamma_2=0 \]

\[ z_i=\frac{g_i-0}{\sigma_{g_i}} \ \ \ \ 临界值z_{1-\alpha/2} \]

7.2.2.4 Shapiro-Wilk检验（小样本）

Show the code
shapiro.test(df$low)  
#> 
#>  Shapiro-Wilk normality test
#> 
#> data:  df$low
#> W = 0.9718, p-value = 0.8867
shapiro.test(df$medium)  
#> 
#>  Shapiro-Wilk normality test
#> 
#> data:  df$medium
#> W = 0.96762, p-value = 0.8598
shapiro.test(df$high)  
#> 
#>  Shapiro-Wilk normality test
#> 
#> data:  df$high
#> W = 0.94361, p-value = 0.6916

# 因为观测太少，也可以同时检验
shapiro.test(c(df$low,df$medium,df$high))  
#> 
#>  Shapiro-Wilk normality test
#> 
#> data:  c(df$low, df$medium, df$high)
#> W = 0.94559, p-value = 0.4578

7.2.2.5 Kolmogorov-Smirnov检验（Lilliefors correction 大样本）

Show the code
ks.test(c(df$low,df$medium,df$high),"pnorm")
#> 
#>  Exact one-sample Kolmogorov-Smirnov test
#> 
#> data:  c(df$low, df$medium, df$high)
#> D = 1, p-value < 2.2e-16
#> alternative hypothesis: two-sided
ks.test(rnorm(1000),"pnorm")
#> 
#>  Asymptotic one-sample Kolmogorov-Smirnov test
#> 
#> data:  rnorm(1000)
#> D = 0.036487, p-value = 0.1395
#> alternative hypothesis: two-sided
Show the code
x <- rnorm(50) 
y <- runif(50) 
ks.test(x, y)  # perform ks test
#> 
#>  Exact two-sample Kolmogorov-Smirnov test
#> 
#> data:  x and y
#> D = 0.46, p-value = 3.801e-05
#> alternative hypothesis: two-sided

x <- rnorm(50)
y <- rnorm(50)
ks.test(x, y) 
#> 
#>  Exact two-sample Kolmogorov-Smirnov test
#> 
#> data:  x and y
#> D = 0.1, p-value = 0.9667
#> alternative hypothesis: two-sided

7.2.3 方差齐性

http://www.cookbook-r.com/Statistical_analysis/Homogeneity_of_variance/

7.2.3.1 Bartlett’s test

数据满足正态性

比较每一组方差的加权算术均值和几何均值。

\[ H_0:\sigma_1^2=\sigma_2^2=...=\sigma_k^2 \] 当样本量\(n_j\)≥5时，检验统计量(各组样本量相等)

\[ B=\frac{(n-1)[kln\bar S^2-\sum_{j=1}^{k}lnS_j^2]}{1+\frac{k+1}{3k(n-1)}} \sim\ \chi^2(\nu)\ ,\nu=k-1 \] 其中n是每一组的样本量，\(S_j^2\)是某一组的样本方差，\(\bar S^2\)是所有k个组样本方差的平均值。

当各组样本量不等时，

\[ B=\frac{\sum_{j=1}^{k}(n_j-1)ln\frac{\bar S^2}{S_j^2}}{1+\frac{1}{3(k-1)}(\sum_{j=1}^{k}\frac {1}{n_j-1}-\frac{1}{\sum_{j=1}^{k}(n_j-1)})} \sim\ \chi^2(\nu)\ ,\nu=k-1 \] 其中\(h_j\)是某一组的样本量，\(\bar S^2=(\sum_{j=1}^{k}(n_j-1)S_j^2)/(\sum_{j=1}^{k}(n_j-1))\)是所有k个组样本方差的加权平均值。

Show the code
n1=n2=n3=5
k=3
S2 <- apply(df,2,var)
S2
#>    low medium   high 
#> 25.372 23.895 26.257

lnS2 <- log(S2)
lnS2
#>      low   medium     high 
#> 3.233646 3.173669 3.267933

S2_mean <- (5-1)*(sum(S2))/(3*(5-1))
S2_mean
#> [1] 25.17467



B <- ((5-1)*(3*log(S2_mean)-sum(lnS2)))/(1+(3+1)/(3*3*(5-1)))
B
#> [1] 0.008159536
Show the code
bartlett.test(df)
#> 
#>  Bartlett test of homogeneity of variances
#> 
#> data:  df
#> Bartlett's K-squared = 0.0081595, df = 2, p-value = 0.9959

7.2.3.2 Levene’s test

数据不满足正态性

  1. k个随机样本是独立的
  2. 随机变量X是连续的

Levene 变换：

\[ Z_{ij}=|X_{ij}-\bar X_{.\ j}|(i=1,2...,n_j;\ j=1,2,...,k) \]

Show the code
options(digits = 2)
z_df <- bind_cols(
    low=df[1]-k_means[1],
    medium=df[2]-k_means[2],
    high=df[3]-k_means[3]
) |> abs()
    

z_df
#>    low medium high
#> 1 3.48    3.2  3.5
#> 2 6.32    0.6  6.9
#> 3 3.52    6.1  3.6
#> 4 0.28    3.6  1.4
#> 5 6.08    5.9  5.5

检验统计量（基于变换后的F检验）

\[ W=\frac{MS_{组间}}{MS_{组内}}=\frac{\sum_jn_j(\bar Z_{.j}-\bar Z_{..})^2/(k-1)}{\sum_j\sum_i(Z_{ij}-\bar Z_{.j})^2/(n-k)} \sim F(\nu_1,\nu_2) \ \ \ \ \nu_1=k-1,\nu_2=n-k \]

Show the code
v1=3-1
v2=15-3


z.j_mean <- apply(z_df, 2, mean)
z.j_mean
#>    low medium   high 
#>    3.9    3.9    4.2

z_mean <- mean(z.j_mean)
z_mean 
#> [1] 4

options(digits = 4)
W <- 12*sum(5*(z.j_mean-z_mean)^2)/(2*(sum((z_df$low-z.j_mean[1])^2)+sum((z_df$medium-z.j_mean[2])^2)+sum((z_df$high-z.j_mean[3])^2)))

W
#> [1] 0.0254

7.3 Welch’s ANOVA Test

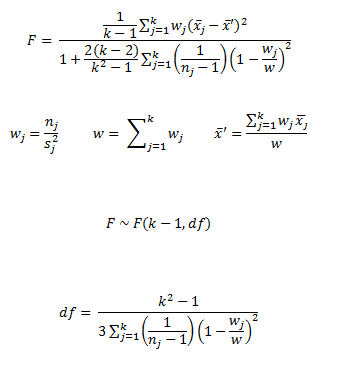
7.4 数据变换

当方差分析的正态性假设或方差齐性假设不为真时，通常使用(1)数据变换方法；(2)非参数检验方法 比较均值差异

7.4.1 平方根变换

当每个水平组的方差与均值成比例，尤其是样本来自泊松分布

\[ Y=\sqrt{X} \]

当数据中有零或非常小的值时，

\[ Y=\sqrt{X+a} \ \ \ \ a=0.5或0.1 \]

7.4.2 对数变换

当数据方差不齐且每个水平组标准差与均值成比例时

\[ Y=\log{X} \ \ \ \ base=e或10 \]

当数据中有零或负值时，

\[ Y=\log{(X+a)} \ \ \ \ a为实数，使得X+a>0 \]

7.4.3 反正弦平方根变换

率，服从二项分布\(B(n,\pi)\)

\[ Y=\arcsin {\sqrt{\pi}} \ \ \ \ \]