医学研究中的生存数据建模
生存函数
\[
S(t)=P(T>t)=1-F(t)=\int_{t}^{+\infty}f(x)dx
\]
其中S(t)是累计生存概率或生存率,量化了生存时间大于t的概率。f(x)是密度函数,呈右偏态分布,反映了任意时间点 t 终点事件的瞬时发生率。F(t)=P(T<t)是f(t)在区间[0,t]的累计形式,也称为分布函数或累积函数。
乘积极限法(Kaplan-Meier)
product limit method 也称为Kaplan-Meier 法。
\(t_1<t_2<t_3<...<t_n\),样本量大小n,ti 代表个体i发生终点事件或右删失的时间。由于一些个体有相同的生存时间,它们被称为 tied 观测时间,生存时间的个数小于样本量n。
点估计S(t)
\(n_1>n_2>n_3>...>n_n\) ,ni d代表在时间点ti 暴露于特定事件风险的幸存者数量。
\(d_i\) 代表在时间点ti 发生终点事件的数量。(如果没有 tie,di=1或0)
生存率的KM方法估计公式:
\[
\hat S(t)=\prod_{t_i\le t}\frac{n_i-d_i}{n_i}
\tag{17.1}\]
Equation 17.1 包括了删失情况,如果从ti-1 到ti 发生了删失,但没有终点事件,di =0,条件概率等于1。
区间估计S(t)
(1-α)×100% CI \([\hat S(t)-z_{1-\alpha/2}\sqrt{Var\left [\hat S(t) \right]},\hat S(t)+z_{1-\alpha/2}\sqrt{Var\left [\hat S(t) \right]}]\)
其中\(Var\left [\hat S(t) \right]=\hat S(t)^2\sum_{t_i\le t}\frac{d_i}{n_i(n_i-d_i)}\) (Greenwood method )
示例
https://biostatsquid.com/easy-survival-analysis-r-tutorial/
Show the code
library(survminer)
library(survival)
library(readr)
library(ggsurvfit)
df <- read_csv("data/log-rank-survival.csv")
surv_obj <- with(df, Surv(Days,status))
surv_fit1 <-survfit(surv_obj ~1,data=df)
# t_i = surv_fit1$time
# n_i = surv_fit1$n.risk
# d_i = surv_fit1$n.event
# cnesored
surv_fit1$n.censor
#> [1] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 17
# 生存率survival
surv_fit1$surv
#> [1] 0.9821429 0.9285714 0.8928571 0.8571429 0.8392857 0.7857143 0.7678571
#> [8] 0.7321429 0.6250000 0.5892857 0.5714286 0.5535714 0.5178571 0.4642857
#> [15] 0.4464286 0.3928571 0.3750000 0.3571429 0.3392857 0.3214286 0.3035714
#> [22] 0.3035714
summary(surv_fit1)
#> Call: survfit(formula = surv_obj ~ 1, data = df)
#>
#> time n.risk n.event survival std.err lower 95% CI upper 95% CI
#> 11 56 1 0.982 0.0177 0.948 1.000
#> 13 55 3 0.929 0.0344 0.864 0.999
#> 14 52 2 0.893 0.0413 0.815 0.978
#> 15 50 2 0.857 0.0468 0.770 0.954
#> 16 48 1 0.839 0.0491 0.748 0.941
#> 17 47 3 0.786 0.0548 0.685 0.901
#> 18 44 1 0.768 0.0564 0.665 0.887
#> 19 43 2 0.732 0.0592 0.625 0.858
#> 20 41 6 0.625 0.0647 0.510 0.766
#> 21 35 2 0.589 0.0657 0.474 0.733
#> 23 33 1 0.571 0.0661 0.455 0.717
#> 24 32 1 0.554 0.0664 0.438 0.700
#> 25 31 2 0.518 0.0668 0.402 0.667
#> 27 29 3 0.464 0.0666 0.350 0.615
#> 28 26 1 0.446 0.0664 0.333 0.598
#> 30 25 3 0.393 0.0653 0.284 0.544
#> 32 22 1 0.375 0.0647 0.267 0.526
#> 38 21 1 0.357 0.0640 0.251 0.508
#> 39 20 1 0.339 0.0633 0.235 0.489
#> 40 19 1 0.321 0.0624 0.220 0.470
#> 45 18 1 0.304 0.0614 0.204 0.451
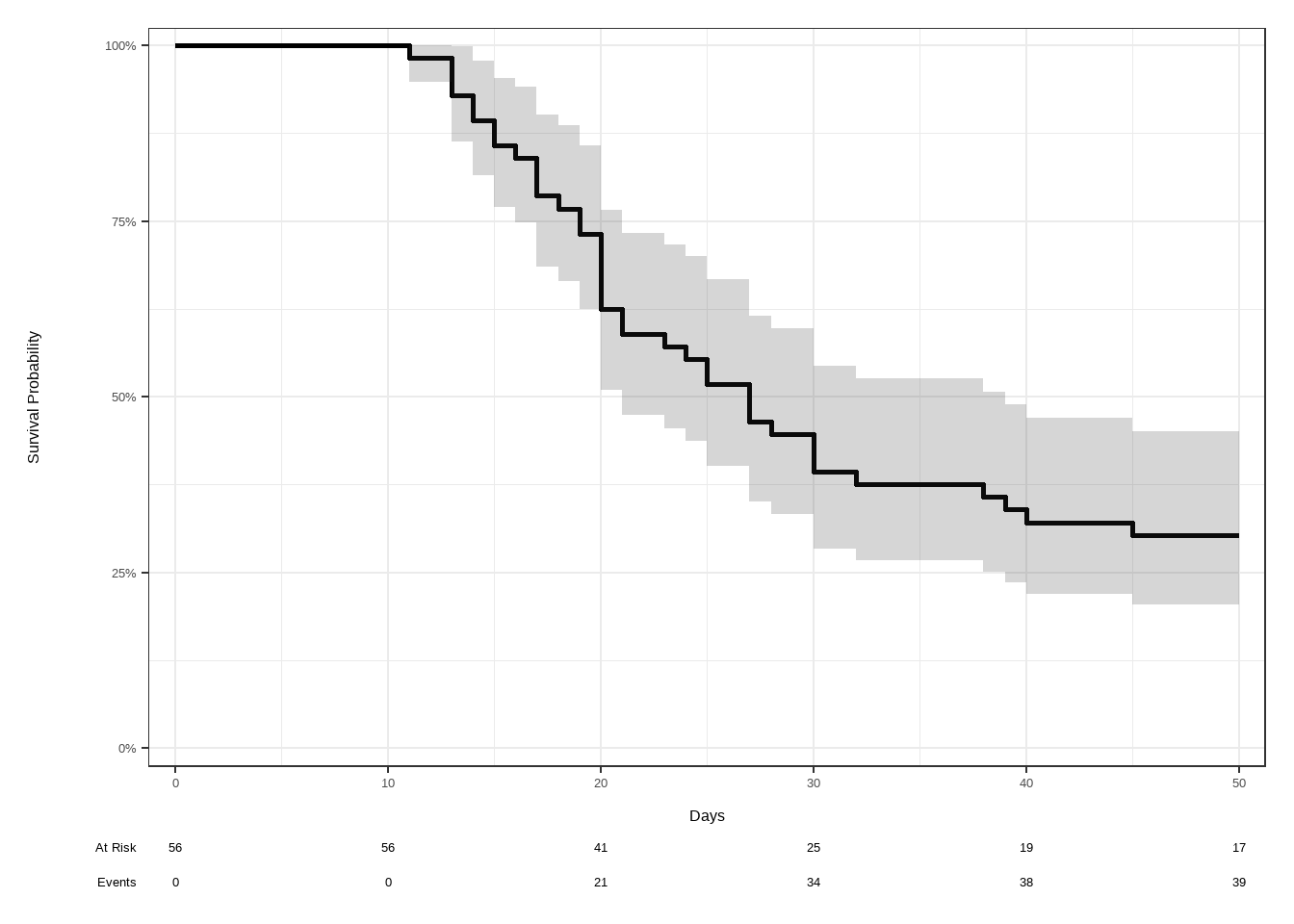
ggsurvfit(surv_fit1, linewidth =1)+
add_confidence_interval()+
scale_ggsurvfit()+
add_risktable() +
labs(x = "Days")
Show the code
# 估计 x-天 的生存率
summary( surv_fit1, times = c(0,30,50))$surv
#> [1] 1.0000000 0.3928571 0.3035714
# 中位生存率 median
surv_fit1
#> Call: survfit(formula = surv_obj ~ 1, data = df)
#>
#> n events median 0.95LCL 0.95UCL
#> [1,] 56 39 27 21 39
单因素生存曲线的比较
| log-rank test |
1 |
| Wilcoxon test |
nj
|
| Tarone-Ware test |
\(\sqrt{n_j}\) |
| Peto test |
\(\hat S(t_j)\) |
\[
\chi^2=\frac{\left(\sum_jw(t_j)(m_{ij}-e_{ij})\right)^2}{\hat {Var}\left(\sum_jw(t_j)(m_{ij}-e_{ij})\right)}
\]
log-rank test
H0 :两总体的生存曲线是相同的。
-
计算当第j次发生终点事件各组终点事件的期望值(e1j ,e2j )
\(e_{1j}=\left ( \frac{n_{1j}}{n_{1j}+n_{2j}}\right)\times (m_{1j}+m_{2j})\)
\(e_{2j}=\left ( \frac{n_{2j}}{n_{1j}+n_{2j}}\right)\times (m_{1j}+m_{2j})\)
其中mij 表示在第 j 个时间点第 i 组终点事件的数量,nij 表示在第 j 个时间点第 i 组初始观测的数量
-
对所有时间点对终点事件的观测值和期望值的差异求和
\(O_i-Ei=\sum_j(m_{ij}-e_{ij})\ \ \ (i=1,2)\)
计算其方差估计值
\(\hat{Var}=\sum_j\frac{n_{1j}n_{2j}(m_{1j}+m_{2j})(n_{1j}+n_{2j}-m_{1j}-m_{2j})}{(n_{1j}+n_{2j})^2(n_{1j}+n_{2j}-1)}\ \ \ (i=1,2)\)
-
计算log-rank test 的检验统计量
\[
\chi^2=\frac{(O_1-E_1)^2}{\hat{Var}(O_1-E_1)} \ 或者 \ \chi^2=\frac{(O_2-E_2)^2}{\hat{Var}(O_2-E_2)}
\]
也可以近似估计为
\[
\chi^2=\sum_{i=1}^2\frac{(O_i-E_i)^2}{E_i} \sim \chi^2(\nu=1)
\]
Show the code
surv_fit2<-survfit(surv_obj ~ treatment,data=df)
ggsurvplot(surv_fit2, linewidth =1,
data = df,
censor.shape = "|", censor.size = 4,
pval = T,conf.int = T,risk.table = T,risk.table.col = "strata",
legend.labs = c("CON","DPVB","LDRT","LR-DPVB"),
risk.table.height = .25,
ggtheme = theme_bw()
)+
labs(x = "Days")
#> NULL
Show the code
# 执行Log-rank检验
logrank_test <- survdiff( Surv(Days,status) ~ treatment,data = df)
logrank_test
#> Call:
#> survdiff(formula = Surv(Days, status) ~ treatment, data = df)
#>
#> N Observed Expected (O-E)^2/E (O-E)^2/V
#> treatment=CON 14 14 4.46 20.40 26.03
#> treatment=DPVB 14 9 13.26 1.37 2.19
#> treatment=LDRT 14 14 5.53 12.99 16.92
#> treatment=LR_DPVB 14 2 15.76 12.01 22.67
#>
#> Chisq= 58.4 on 3 degrees of freedom, p= 1e-12
logrank_test$chisq
#> [1] 58.43627
logrank_test$pvalue
#> [1] 1.268397e-12
Show the code
survdiff( Surv(Days,status) ~ treatment,
data = df |> dplyr::filter(treatment %in% c("CON", "DPVB")))
#> Call:
#> survdiff(formula = Surv(Days, status) ~ treatment, data = dplyr::filter(df,
#> treatment %in% c("CON", "DPVB")))
#>
#> N Observed Expected (O-E)^2/E (O-E)^2/V
#> treatment=CON 14 14 5.3 14.31 24.1
#> treatment=DPVB 14 9 17.7 4.28 24.1
#>
#> Chisq= 24.1 on 1 degrees of freedom, p= 9e-07
survdiff( Surv(Days,status) ~ treatment,
data = df |> dplyr::filter(treatment %in% c("CON", "LDRT")))
#> Call:
#> survdiff(formula = Surv(Days, status) ~ treatment, data = dplyr::filter(df,
#> treatment %in% c("CON", "LDRT")))
#>
#> N Observed Expected (O-E)^2/E (O-E)^2/V
#> treatment=CON 14 14 12 0.331 0.716
#> treatment=LDRT 14 14 16 0.248 0.716
#>
#> Chisq= 0.7 on 1 degrees of freedom, p= 0.4
survdiff( Surv(Days,status) ~ treatment,
data = df |> dplyr::filter(treatment %in% c("CON", "LR_DPVB")))
#> Call:
#> survdiff(formula = Surv(Days, status) ~ treatment, data = dplyr::filter(df,
#> treatment %in% c("CON", "LR_DPVB")))
#>
#> N Observed Expected (O-E)^2/E (O-E)^2/V
#> treatment=CON 14 14 4.73 18.16 31.1
#> treatment=LR_DPVB 14 2 11.27 7.62 31.1
#>
#> Chisq= 31.1 on 1 degrees of freedom, p= 2e-08