Show the code
Show the code
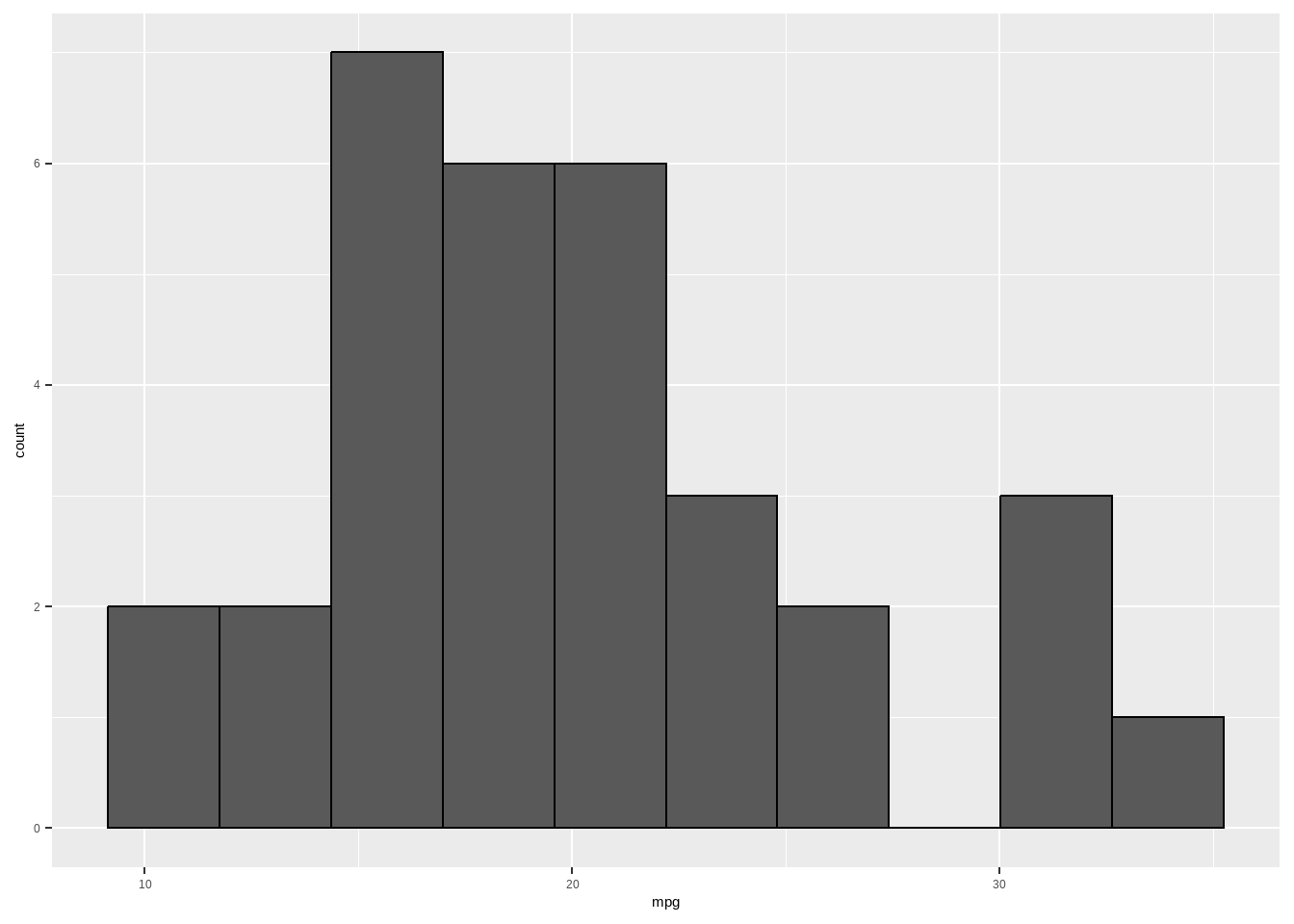
ggplot(data = mtcars, aes(x = mpg)) +
geom_histogram(color = "black", binwidth = diff(range(mtcars$mpg)) / 9)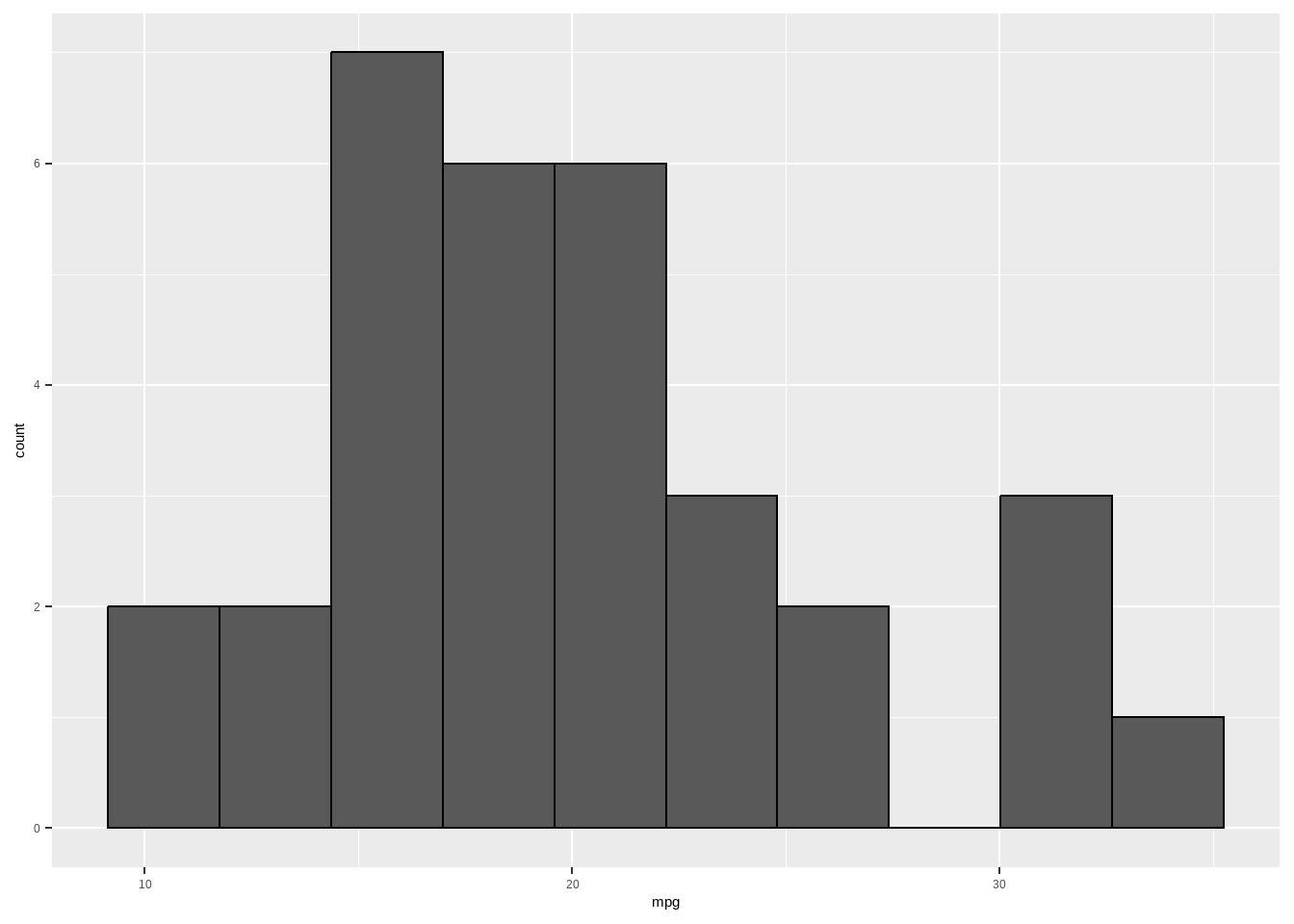
极差(Range) : \(R=X_{max}-X_{min}\)
组数 (Number of Bins) \(k\) : 通常选择 \(8\) 到 \(15\) 之间的值。
组距 (Bin Width) : \(interval=\frac{R}{k}\)
频数 (Frequency) : \(Frequency = count\)
频率 (Relative Frequency): \(Relative\ Frequency = \frac{count}{n} \times 100\%\)
总体方差除以 n
样本方差除以(n-1),R 计算的是样本方差
x <- c(1,2:9,11)
#算术均值
mean(x)
#> [1] 5.6
sum(x)/length(x)
#> [1] 5.6
# 截尾均值 10%,则只有 80% 的中心数据将用于计算平均值。
mean(x,trim = 0.1)
#> [1] 5.5
# 加权平均值
z <- c(5, 7, 8)
# 权重(和为1)
wts <- c(0.2, 0.2, 0.6)
weighted.mean(z, w = wts)
#> [1] 7.2
sum(z * wts)
#> [1] 7.2
# 几何平均值
w <- c(10, 20, 15, 40)
# Geometric mean
exp(mean(log(w)))
#> [1] 18.6121
psych::geometric.mean(w)
#> [1] 18.6121注意:函数rstatix::get_mode() 可能返回多个众数,如果存在多个众数,请检查其处理方式。
# 值域
range(mtcars$mpg)
#> [1] 10.4 33.9
# 极差 or 全距
diff(range(mtcars$mpg) )
#> [1] 23.5
# 方差 variance
var(mtcars$mpg)
#> [1] 36.3241
# 标准差 standard deviation
sd(mtcars$mpg)
#> [1] 6.026948
# 变异系数 Coefficient of Variation
CV <- function(x, na.rm = TRUE) {
if (na.rm) x <- x[!is.na(x)]
CV = sd(x) / abs(mean(x)) * 100
sprintf("%.8f%%", CV)
}
CV(mtcars$mpg)
#> [1] "29.99880816%"
# 绝对中位差 median absolute deviation
mad(mtcars$mpg,constant = 1.4826)
#> [1] 5.41149
median(abs(mtcars$mpg-median(mtcars$mpg)))
#> [1] 3.65
median(abs(mtcars$mpg-median(mtcars$mpg)))*1.4826
#> [1] 5.41149说明:mad() 计算时乘以比例因子 constant = 1.4826 以实现渐进正态一致性。
# 协方差系数
cov(mpg %>% select(displ,cty,hwy))
#> displ cty hwy
#> displ 1.669158 -4.39069 -5.893111
#> cty -4.390690 18.11307 24.225432
#> hwy -5.893111 24.22543 35.457779
cov(mpg %>% select(displ,cty,hwy)) %>% cov2cor()
#> displ cty hwy
#> displ 1.000000 -0.7985240 -0.7660200
#> cty -0.798524 1.0000000 0.9559159
#> hwy -0.766020 0.9559159 1.0000000
# Pearson 相关系数
cor(mpg %>% select(displ,cty,hwy))
#> displ cty hwy
#> displ 1.000000 -0.7985240 -0.7660200
#> cty -0.798524 1.0000000 0.9559159
#> hwy -0.766020 0.9559159 1.0000000
# Kendall 的 tau 相关系数 适用于有序数据或非正态分布数据,因为它基于值的排名或顺序,而不是实际值。
cor(mpg %>% select(displ,cty,hwy), method = "kendall")
#> displ cty hwy
#> displ 1.0000000 -0.7210828 -0.6536974
#> cty -0.7210828 1.0000000 0.8628045
#> hwy -0.6536974 0.8628045 1.0000000
# Spearman 的 rho 相关系数 Pearson 系数的稳健非参数替代项,数据非正态或具有异常值
cor(mpg %>% select(displ,cty,hwy), method = "spearman")
#> displ cty hwy
#> displ 1.0000000 -0.8809049 -0.8266576
#> cty -0.8809049 1.0000000 0.9542104
#> hwy -0.8266576 0.9542104 1.0000000表示随机变量概率分布的不对称性。
https://www.macroption.com/skewness-formula/
三阶中心矩。二阶中心矩即方差。
\[ Population\ Skewness (X) = \frac{E(X_i-E(X))^3}{Var(X)^{\frac{3}{2}}} =E [(\frac{X_i-\mu}{\sigma})^3]= \frac{1}{n} \sum_{i=1}^{n} (\frac{X_i-\mu}{\sigma} )^3 \]
偏度的取值范围: \((-\infty,+\infty)\)
Skew>0,正偏态分布,右偏 = 尾部向右延伸。Mode < Median < Mean;
Skew=0,数据相对均匀的分布在均值两侧;
Skew<0,负偏态分布,左偏 = 尾部向左延伸;Mode > Median > Mean。
x <- c(1,2,3,5,6,10)
skewness <- function(x,na.rm=TRUE){
if(na.rm) x <- x[!is.na(x)]
n=length(x)
μ=mean(x)
SD=sd(x)
return(c(population_sknewness = mean(((x-μ)/SD)^3),
sample_sknewness = sum(((x-μ)/SD)^3)*n/(n-1)/(n-2)))
}
skewness(x)
#> population_sknewness sample_sknewness
#> 0.5142767 0.9256980
e1071::skewness(x,type = 2) # 样本偏度
#> [1] 0.925698
e1071::skewness(x,type = 3) # 总体偏度
#> [1] 0.5142767
e1071::skewness(x,type = 1) # 无偏偏度
#> [1] 0.6760343
moments::skewness(x)
#> [1] 0.6760343\[ Sample\ Skewness(X) = \frac{n}{(n-1)(n-2)} \sum_{i=1}^{n} \left [\frac{X_i-\bar X}{S} \right ]^3 \]
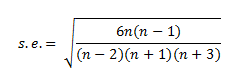
表示随机变量概率分布的尖峭程度。四阶中心矩与方差平方的比值。
https://www.macroption.com/kurtosis-formula/
超额峰度 excess kurtosis :四阶中心矩与方差平方的比值减3。
https://www.macroption.com/excess-kurtosis/
\[ Population\ Kurtosis(X) = \frac{E(X_i-E(X))^4}{Var(X)^{2}}-3= E [(\frac{X_i-\mu}{\sigma})^4] - 3= \frac{1}{n} \sum_{i=1}^{n} (\frac{X_i-\mu}{\sigma} )^4-3 \]
超额峰度的取值范围:\([-2,+\infty)\)
超额峰度<0,数据分布与正态分布相比较为扁平;
超额峰度=0,正态分布;
超额峰度>0,数据分布与正态分布相比较为高尖。
kurtosis<-function(x,na.rm=TRUE){
if(na.rm) x<-x[!is.na(x)]
n=length(x)
μ=mean(x)
SD=sd(x)
return(c(population_kurtosis= mean(((x-μ)/SD)^4)-3,
sample_kurtosis = sum(((x-μ)/SD)^4)*n*(n+1)/(n-1)/(n-2)/(n-3)-3*(n-1)^2/(n-2)/(n-3)))
}
kurtosis(x)
#> population_kurtosis sample_kurtosis
#> -1.377770 0.563368
e1071::kurtosis(x,type = 3)# 默认
#> [1] -1.37777
e1071::kurtosis(x,type = 2)
#> [1] 0.563368\[ Sample \ Kurtosis(X) = \frac{n(n+1)}{(n-1)(n-2)(n-3)} \sum_{i=1}^{n} \left [\frac{X_i-\bar X}{S} \right]^4-\frac{3(n-1)^2}{(n-2)(n-3)} \]
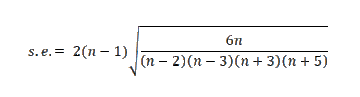
summary(mtcars$mpg)
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 10.40 15.43 19.20 20.09 22.80 33.90
rstatix::get_summary_stats(mtcars,mpg,type = "full")
#> # A tibble: 1 × 13
#> variable n min max median q1 q3 iqr mad mean sd se
#> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 mpg 32 10.4 33.9 19.2 15.4 22.8 7.38 5.41 20.1 6.03 1.06
#> # ℹ 1 more variable: ci <dbl>
psych::describeBy(mtcars$mpg,group =NULL)
#> vars n mean sd median trimmed mad min max range skew kurtosis se
#> X1 1 32 20.09 6.03 19.2 19.7 5.41 10.4 33.9 23.5 0.61 -0.37 1.07