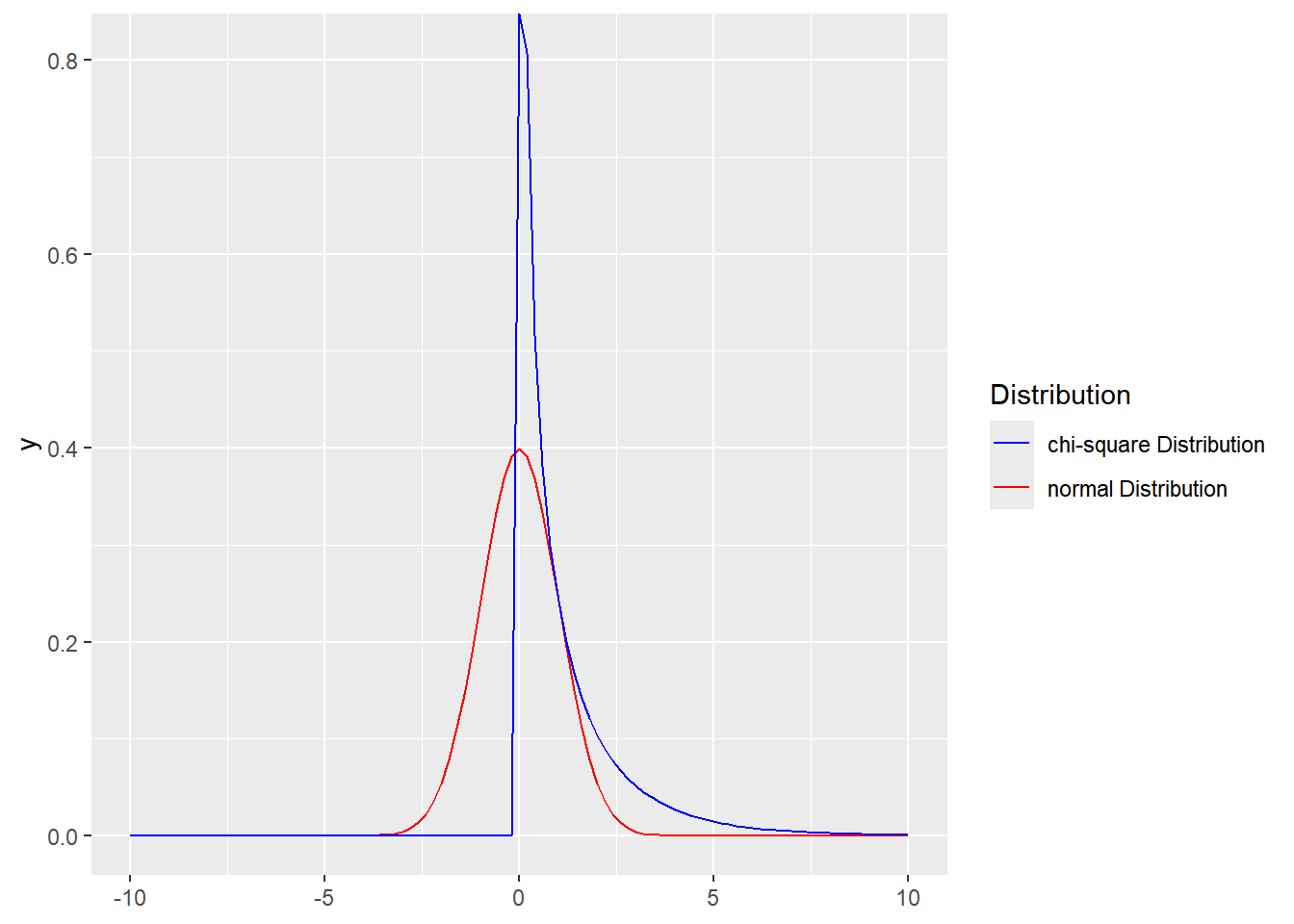
卡方分布
卡方分布可以通过原假设,得到一个统计量来表示期望结果和实际结果之间的偏离程度,进而根据分布,自由度和假设成立的情况,得出观察频率极值的发生概率(比当前统计结果更加极端的概率)。计算方法是对概率分布中的每个频率,用期望频数和实际频数差的平方除以期望频数,最后把所有结果相加。
\[ \chi^2=\sum \frac {(O-E)^2} {E} \]
得到的统计量结果越大,说明差别越显著,数值越小说明观察和期望的差别越小,当观察频数和期望频数一致是卡方为0。其实就是在比较观测到的比例和期望的比例的关系。
Show the code ggplot ( ) + xlim ( - 10 ,10 ) + geom_function ( mapping = aes ( color= "normal Distribution" ) ,
fun = dnorm , args = list ( mean = 0 , sd = 1 ) ,
) +
geom_function ( mapping = aes ( color= "chi-square Distribution" ) ,
fun = dchisq , args = list ( df = 1 ,ncp= 0 ) ,
) +
scale_color_manual ( values = c ( "normal Distribution" = "red" ,
"chi-square Distribution" = "blue" ) ) +
labs ( color = "Distribution" )
卡方分布就可以用来检验某个分类变量各类的出现概率是否等于指定概率,可以检验数据的拟合优度(指定的一组数据与指定分布的吻合度),也可以用来检验两个变量的独立性(两个变量之间是否存在某种关联)。
在使用卡方检验时,需要的一个参数被称为自由度,指的是独立变量的个数(组数减去限制数)。通常,二项分布已知 \(\pi\) ,泊松分布已知 \(\lambda\) ,正态分布已知 \(\mu\) 和 \(\sigma^2\) 时的自由度是n-1。进行独立性检验时,n行m列联列表的自由度是(n-1) x (m-1)。
Pearson’s \(\chi^2\) 检验 用于检验涉及双向无序多分类变量 的概率或比例。
2×2列联表
独立性:判断两个或多个分类变量之间是否存在关联或取值互不影响,分析联合概率分布是否可以分解为各自概率分布的乘积。
卡方检验
对于频数表中每个单元格的期望频数都比较大(大于 5)的大样本,correct设为FALSE,不进行连续校正。
Show the code x <- matrix ( c ( 97 ,73 ,7 ,30 ) ,2 ,dimnames = list ( c ( "experiment" ,"control" ) ,c ( "+" ,"-" ) ) ) x #> + - #> experiment 97 7 #> control 73 30 ( k1 <- chisq.test ( x ,correct = F ) ) #> #> Pearson's Chi-squared test #> #> data: x #> X-squared = 17.681, df = 1, p-value = 2.612e-05 # 期望频数列联表 k1 $ expected #> + - #> experiment 85.41063 18.58937 #> control 84.58937 18.41063 k1 $ parameter # degrees of freedom #> df #> 1
Yate’s 校正
某些单元格的期望频数接近于或小于 5 时,进行 Yates’ 连续校正以修正卡方统计量提高准确性。
Show the code x <- matrix ( c ( 1004 , 325 , 20 , 1 ) , 2 , dimnames = list ( c ( "experiment" , "control" ) , c ( "+" , "-" ) ) )
x #> + - #> experiment 1004 20 #> control 325 1 chisq.test ( x ,correct = F ) $ expected #> + - #> experiment 1008.0711 15.928889 #> control 320.9289 5.071111 # 校正 ( k2 <- chisq.test ( x ,correct = T ) ) #> #> Pearson's Chi-squared test with Yates' continuity correction #> #> data: x #> X-squared = 3.3678, df = 1, p-value = 0.06648
Fisher’s Exact 检验
Fisher 精确概率检验(Fisher’s Exact Test)通常在以下情况中使用:
总样本数 n 小于 40;
列联表中任何一个单元格的期望频数小于 5。
Show the code x <- matrix ( c ( 7 ,2 ,7 ,17 ) ,2 ,dimnames = list ( c ( "A" ,"B" ) ,c ( "Yes" ,"No" ) ) ) x #> Yes No #> A 7 7 #> B 2 17 ( k5 <- fisher.test ( x ) ) #> #> Fisher's Exact Test for Count Data #> #> data: x #> p-value = 0.01914 #> alternative hypothesis: true odds ratio is not equal to 1 #> 95 percent confidence interval: #> 1.134346 96.442876 #> sample estimates: #> odds ratio #> 7.892809 chisq.test ( x )
#> #> Pearson's Chi-squared test with Yates' continuity correction #> #> data: x #> X-squared = 4.4985, df = 1, p-value = 0.03393 E <- chisq.test ( x ) $ expected chisq <- sum ( ( x - E ) ^ 2 / E ) chisq #> [1] 6.332237 p_value_asymptotic <- 1 - pchisq ( chisq , df = 1 )
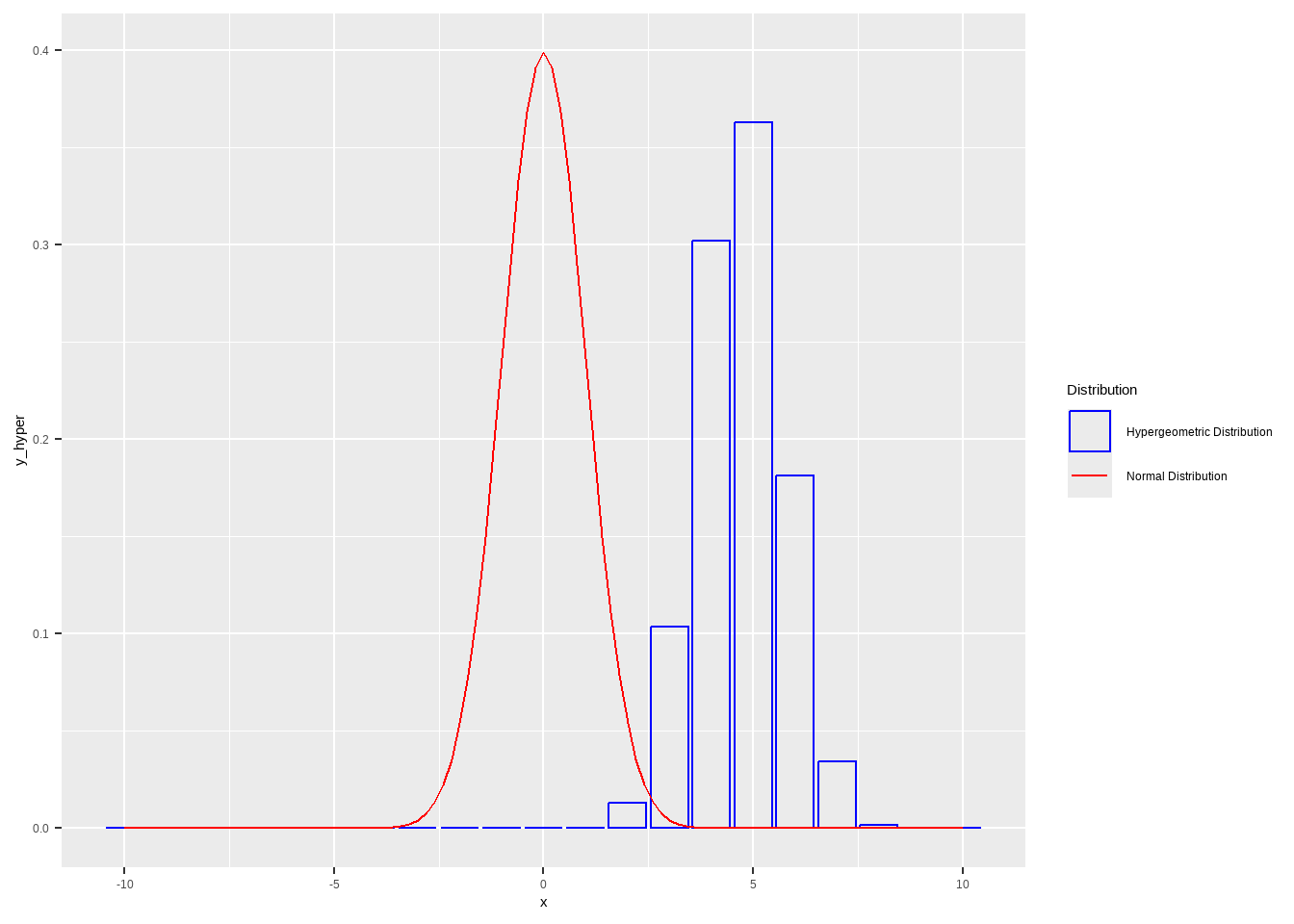
超几何分布
Show the code tibble ( x = - 10 : 10 ,
y_hyper = dhyper ( x , m = 10 ,n = 7 ,k = 8 ) ,
) %>% ggplot ( ) +
geom_col ( aes ( x= x ,y = y_hyper ,color= "Hypergeometric Distribution" ) ,fill= NA ) +
geom_function ( aes ( color= "Normal Distribution" ) ,
fun= dnorm , args = list ( mean = 0 , sd = 1 ) ) +
scale_color_manual ( values = c ( "Normal Distribution" = "red" ,
"Hypergeometric Distribution" = "blue" ) ) +
labs ( color = "Distribution" )
配对四格表
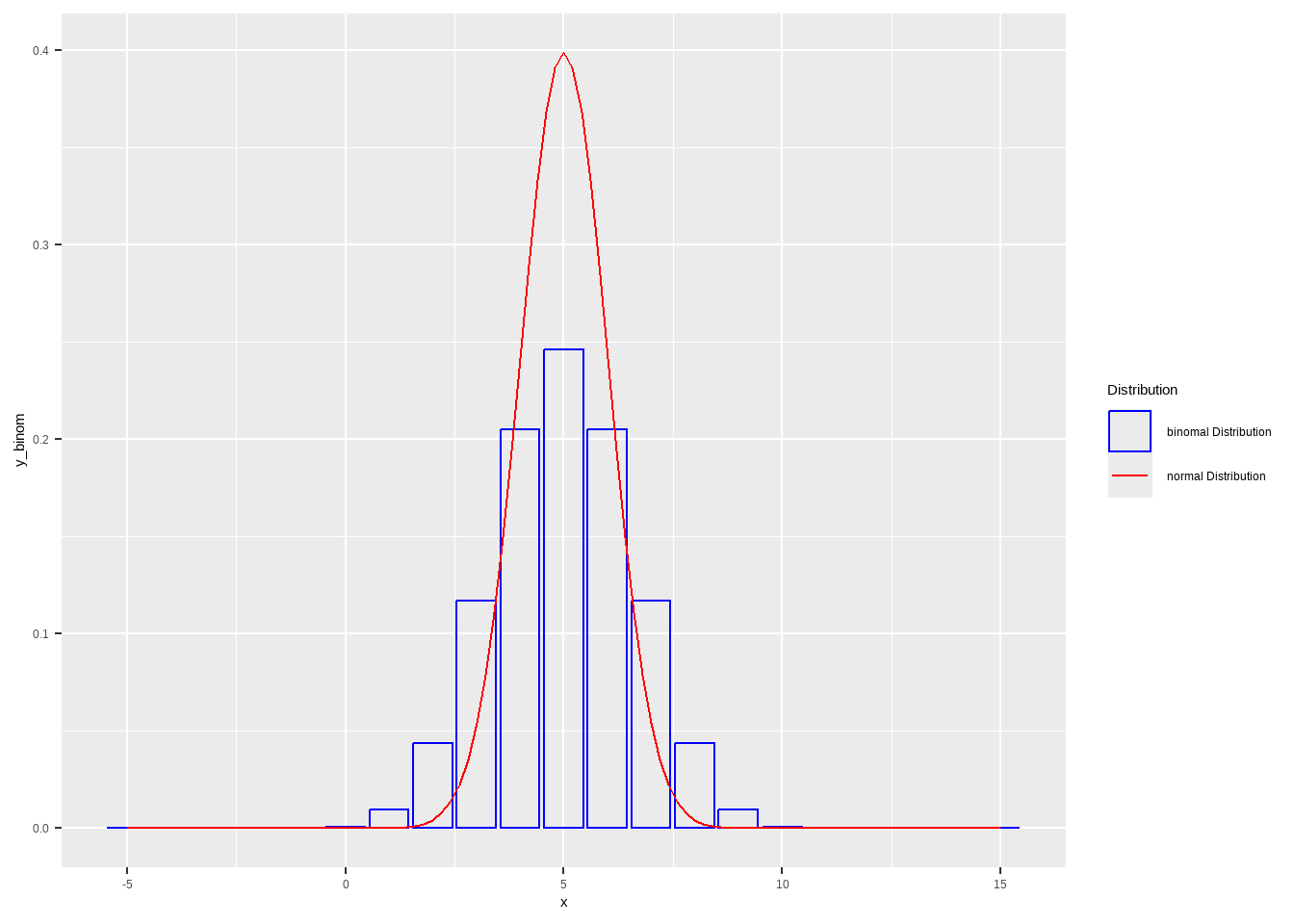
二项分布
Show the code tibble ( x = - 5 : 15 ,
y_binom = dbinom ( x , size = 10 ,prob = 0.5 ) ,
) %>% ggplot ( ) + geom_col ( aes ( x= x ,y= y_binom ,color= "binomal Distribution" ) ,fill= NA ) +
geom_function ( mapping = aes ( color= "normal Distribution" ) ,
fun = dnorm , args = list ( mean = 5 , sd = 1 ) ,
) +
scale_color_manual ( values = c ( "normal Distribution" = "red" ,
"binomal Distribution" = "blue" ) ) +
labs ( color = "Distribution" )
McNemar’s 检验
20 < b+c = 5 + 34 < 40
Show the code x <- matrix ( c ( 36 ,34 ,5 ,135 ) ,2 ,dimnames = list ( c ( "A+" ,"A-" ) ,c ( "B+" ,"B-" ) ) ) x #> B+ B- #> A+ 36 5 #> A- 34 135 ( k3 <- mcnemar.test ( x ,correct = F ) ) #> #> McNemar's Chi-squared test #> #> data: x #> McNemar's chi-squared = 21.564, df = 1, p-value = 3.422e-06 # 对于配对四格表,如果样本量较小(不一致的结果的总数小于 40 ) ,则需要进行连续性校正。 ( k4 <- mcnemar.test ( x ,correct = T ) ) #> #> McNemar's Chi-squared test with continuity correction #> #> data: x #> McNemar's chi-squared = 20.103, df = 1, p-value = 7.34e-06
Show the code # 某实验室分别用免疫荧光法和乳胶凝集法对 58 名疑似系统性红斑狼疮患者血清中抗 核抗体进行测定 result <- matrix ( c ( 11 , 2 , 12 , 33 ) , nrow = 2 ,dimnames = list ( c ( "+" ,"-" ) ,c ( "+" ,"-" ) ) ) result #> + - #> + 11 12 #> - 2 33 # 对于配对四格表,如果样本量较小(不一致的结果的总数小于 40 ) ,则需要进行连续性校正。 mcnemar.test ( result ,correct = TRUE ) #> #> McNemar's Chi-squared test with continuity correction #> #> data: result #> McNemar's chi-squared = 5.7857, df = 1, p-value = 0.01616
精确 McNemar’s 检验
b+c = 7 + 1 <20
二项分布B(b+c,0.5),k=min(b,c)
\[
P=\sum_{i≤k} p_i
\]
Show the code x <- matrix ( c ( 3 ,1 ,7 ,9 ) ,2 ,dimnames = list ( c ( "A+" ,"A-" ) ,c ( "B+" ,"B-" ) ) ) x #> B+ B- #> A+ 3 7 #> A- 1 9 P_two_sided <- 2 * sum ( dbinom ( x= 0 : 1 ,size = 8 ,prob = 0.5 ) ) P_two_sided #> [1] 0.0703125
R×C列联表
卡方检验
在 R×C 列联表的情况下,如果表中的单元格期望频数满足以下条件:
期望频数 T < 5 的单元格不超过 1/5。
没有单元格期望频数 T < 1 。
那么可以选择不进行连续校正
Show the code x <- matrix ( c ( 150 ,184 ,198 ,50 ,16 ,2 ) ,3 ,dimnames = list ( c ( "A" ,"B" ,"C" ) ,c ( "Yes" ,"No" ) ) ) x #> Yes No #> A 150 50 #> B 184 16 #> C 198 2 ( k <- chisq.test ( x ,correct = F ) ) #> #> Pearson's Chi-squared test #> #> data: x #> X-squared = 60.637, df = 2, p-value = 6.806e-14
Show the code ( k <- chisq.test ( x ,correct = T ) ) #> #> Pearson's Chi-squared test #> #> data: x #> X-squared = 60.637, df = 2, p-value = 6.806e-14 k $ expected #> Yes No #> A 177.3333 22.66667 #> B 177.3333 22.66667 #> C 177.3333 22.66667
多重比较
\[
\alpha'=\frac {\alpha}{比较的次数=\frac{k(k-1)}{2}}
\]
卡方分割法
卡方分割法与Bonferroni方法调整p值是两种不同的统计分析方法,主要用于处理多重比较问题。它们的区别如下: 1. 卡方分割法 - 定义 :卡方分割法通常用于对卡方检验结果进行后续分析,以确定哪些具体的类别或组之间存在显著差异。该方法基于检验统计量在每对比较中的分布进行分析。 - 应用 :常用于发现哪些特定组(行或列)之间存在差异,通常需要进行后续的成对比较。 - 目的 :帮助识别在显著性结果中,具体是哪些组之间存在显著差异。
Bonferroni方法
定义 :Bonferroni方法是一种用于控制多重比较的显著性水平的校正方法。在进行多次假设检验时,原始的显著性水平(例如0.05)会被除以比较次数,从而得出新的显著性水平。
应用 :适用于多个独立检验结果的显著性水平调整,以减少因多重比较导致的假阳性率。
目的 :降低第一类错误的概率(即假阳性),确保在多次检验中保持整体的显著性水平。
卡方分割法 更侧重于分析具体的类别差异,而Bonferroni方法 则专注于调整p值以控制错误率。
如果你已经通过卡方检验发现某些组之间有显著差异,卡方分割法可以帮助你进一步了解哪些组之间有差异。而Bonferroni方法在初步检验前就帮助控制多重比较的问题,确保分析结果的可靠性。 ’
Show the code # 创建频率矩阵 data <- matrix ( c ( 251 , 225 , 368 , 347 ,
132 , 16 ,
54 , 22 ,
9 , 18 ,
21 , 110 ,
4 , 30 ,
46 , 93 ) ,
nrow = 8 ,
byrow = TRUE )
# 为矩阵添加行和列名称 rownames ( data ) <- c ( "团队" , "球员" , "教练" , "品牌" , "管理" , "历史" , "文化" , "其他" ) colnames ( data ) <- c ( "Period 1" , "Period 2" ) # 执行卡方检验 chi_square_result <- chisq.test ( data , correct= T ) # 显示结果 print ( chi_square_result ) #> #> Pearson's Chi-squared test #> #> data: data #> X-squared = 205.38, df = 7, p-value < 2.2e-16 # 提取卡方值,自由度和p值 chi_square_value <- chi_square_result $ statistic degrees_of_freedom <- chi_square_result $ parameter p_value <- chi_square_result $ p.value # 打印结果 cat ( "卡方值:" , chi_square_value , "\n" ) #> 卡方值: 205.3786 cat ( "自由度:" , degrees_of_freedom , "\n" ) #> 自由度: 7 cat ( "显著性水平 (p值):" , p_value , "\n" ) #> 显著性水平 (p值): 8.326236e-41 # 进行多重卡方检验 chi_square_results <- apply ( data , 1 , function ( x ) chisq.test ( matrix ( x , nrow= 2 ) ) ) # 提取卡方,自由度,p值 X2 <- sapply ( chi_square_results , function ( x ) x $ statistic ) p_values <- sapply ( chi_square_results , function ( x ) x $ p.value ) df <- sapply ( chi_square_results , function ( x ) x $ parameter ) # 多重比较调整 adjusted_p_values <- p.adjust ( p_values , method = "bonferroni" ) signifcance <- case_when (
adjusted_p_values < 0.001 ~ "***" ,
adjusted_p_values < 0.01 ~ "**" ,
adjusted_p_values < 0.05 ~ "*" ,
.default = "ns"
)
results <- tibble ( dimension = rownames ( data ) ,
chisq_statistic = X2 ,
p_value = p_values ,
p_adjust = adjusted_p_values ,
signifcance = signifcance
) print ( results ) #> # A tibble: 8 × 5 #> dimension chisq_statistic p_value p_adjust signifcance #> <chr> <dbl> <dbl> <dbl> <chr> #> 1 团队 1.42 2.33e- 1 1 e+ 0 ns #> 2 球员 0.617 4.32e- 1 1 e+ 0 ns #> 3 教练 90.9 1.50e-21 1.20e-20 *** #> 4 品牌 13.5 2.42e- 4 1.94e- 3 ** #> 5 管理 3 8.33e- 2 6.66e- 1 ns #> 6 历史 60.5 7.49e-15 5.99e-14 *** #> 7 文化 19.9 8.24e- 6 6.59e- 5 *** #> 8 其他 15.9 6.71e- 5 5.36e- 4 ***
拟合优度检验
Pearson’s \(\chi^2\) goodness-of-fit test
此检验检查观察到的频率分布是否与预期的理论分布匹配,例如均匀分布或任何其他预期分布。此检验扩展了单比率 Z 检验 。
Show the code observed <- c ( 11 , 32 , 24 ) # Observed frequencies expected <- c ( 0.2 , 0.5 , 0.3 ) # Expected probabilities (sum up to 1) # Chi-squared test for goodness of fit (Are the population probabilities equal to 'p'?) chisq.test ( x = observed , p = expected ) #> #> Chi-squared test for given probabilities #> #> data: observed #> X-squared = 1.2537, df = 2, p-value = 0.5343
设置rescale.p = TRUE 频率将重新缩放以求和为 1
Show the code observed <- c ( 11 , 32 , 24 ) # Observed frequencies expected <- c ( 20 , 50 , 30 ) # Expected frequencies # Chi-squared test for goodness of fit with rescaled 'p' chisq.test ( x = observed , p = expected , rescale.p = TRUE ) #> #> Chi-squared test for given probabilities #> #> data: observed #> X-squared = 1.2537, df = 2, p-value = 0.5343
如果未指定p,则测试将检查比例是否全部相等(均匀分布)
Show the code observed <- c ( 15 , 25 , 20 ) chisq.test ( observed ) #> #> Chi-squared test for given probabilities #> #> data: observed #> X-squared = 2.5, df = 2, p-value = 0.2865 chisq.test ( observed , p = rep ( 1 / 3 ,3 ) ) #> #> Chi-squared test for given probabilities #> #> data: observed #> X-squared = 2.5, df = 2, p-value = 0.2865
Chi-squared test of homogeneity
此检验比较单个分类变量 在多个独立组或总体 中的分布。它确定单个分类变量的频率分布在不同组中是相似还是同质。此检验扩展了两个比例 Z 检验 。
Show the code data <- matrix ( c ( 18 , 26 , 44 , 6 , 14 , 19 ) , nrow = 2 , byrow = TRUE ) colnames ( data ) <- c ( "Drug A" , "Drug B" , "Drug C" ) rownames ( data ) <- c ( "Age under 30" , "Age over 30" ) chisq.test ( data ) #> #> Pearson's Chi-squared test #> #> data: data #> X-squared = 0.72271, df = 2, p-value = 0.6967 data %>% t ( ) %>% chisq.test ( ) #> #> Pearson's Chi-squared test #> #> data: . #> X-squared = 0.72271, df = 2, p-value = 0.6967
p 值为 0.6967,大于通常的显著性水平,因此没有证据否定年龄组之间分布相等的原假设。
Cochran-Mantel-Haenszel \(\chi^2\) 检验
又叫行均分检验,常用于按照某个变量进行分层后的检验,用于检验两个有序分类变量是否存在线性相关 ,但实际上用途很广泛,比如因变量是有序变量的单向有序列联表,也可以用。
两个变量的关联有可能受到第三个变量的影响,因此我们有必要检验两个分类变量在 调整(控制)第三个变量的情况下是否独立。 Cochran-Mantel-Haenszel χ 2 检验常用于探索 变量间的混杂因素。其零假设是:两个分类变量在第三个变量的每一层都是条件独立的。函数 mantelhaen.test( ) 可以用来进行该检验。
Show the code Rabbits <- array ( c ( 0 , 0 , 6 , 5 , 3 , 0 , 3 , 6 ,
6 , 2 , 0 , 4 ,
5 , 6 , 1 , 0 ,
2 , 5 , 0 , 0 ) ,
dim = c ( 2 , 2 , 5 ) ,
dimnames = list (
Delay = c ( "None" , "1.5h" ) ,
Response = c ( "Cured" , "Died" ) ,
Penicillin.Level = c ( "1/8" , "1/4" , "1/2" , "1" , "4" ) ) )
Rabbits #> , , Penicillin.Level = 1/8 #> #> Response #> Delay Cured Died #> None 0 6 #> 1.5h 0 5 #> #> , , Penicillin.Level = 1/4 #> #> Response #> Delay Cured Died #> None 3 3 #> 1.5h 0 6 #> #> , , Penicillin.Level = 1/2 #> #> Response #> Delay Cured Died #> None 6 0 #> 1.5h 2 4 #> #> , , Penicillin.Level = 1 #> #> Response #> Delay Cured Died #> None 5 1 #> 1.5h 6 0 #> #> , , Penicillin.Level = 4 #> #> Response #> Delay Cured Died #> None 2 0 #> 1.5h 5 0 mantelhaen.test ( Rabbits ) #> #> Mantel-Haenszel chi-squared test with continuity correction #> #> data: Rabbits #> Mantel-Haenszel X-squared = 3.9286, df = 1, p-value = 0.04747 #> alternative hypothesis: true common odds ratio is not equal to 1 #> 95 percent confidence interval: #> 1.026713 47.725133 #> sample estimates: #> common odds ratio #> 7