Mixed Effects Models and Extensions in Ecology with R 第12章
广义估计方程(Generalized Estimating Equations,GEE)是一种用于分析重复测量或相关数据的统计方法。 GEE的核心思想是通过建立一个广义线性模型来估计一组总体均值参数,同时考虑数据的相关性结构和缺失数据,而不依赖于特定的分布假设,从而使其适用于多种数据类型,包括二项分布、正态分布、负二项分布。
广义估计方程用于处理具有组内相关性的非正态分布数据。模型形式类似于广义线性模型,但使用了估计方程来考虑组内相关性。
数据集下载
数据集 Analyzing ecological data
Show the code rfb <- read_delim ( "data/AED/RiceFieldBirds.txt" ) rfb $ richness <- rowSums ( rfb [ , 8 : 56 ] > 0 ) rfb |> mutate ( FIELD = factor ( FIELD ) ,
SPTREAT = factor ( SPTREAT ) ,
log_AREA = log ( rfb $ AREA ) ,
DEPTH2 = DEPTH ^ 2 ,
.after = 4
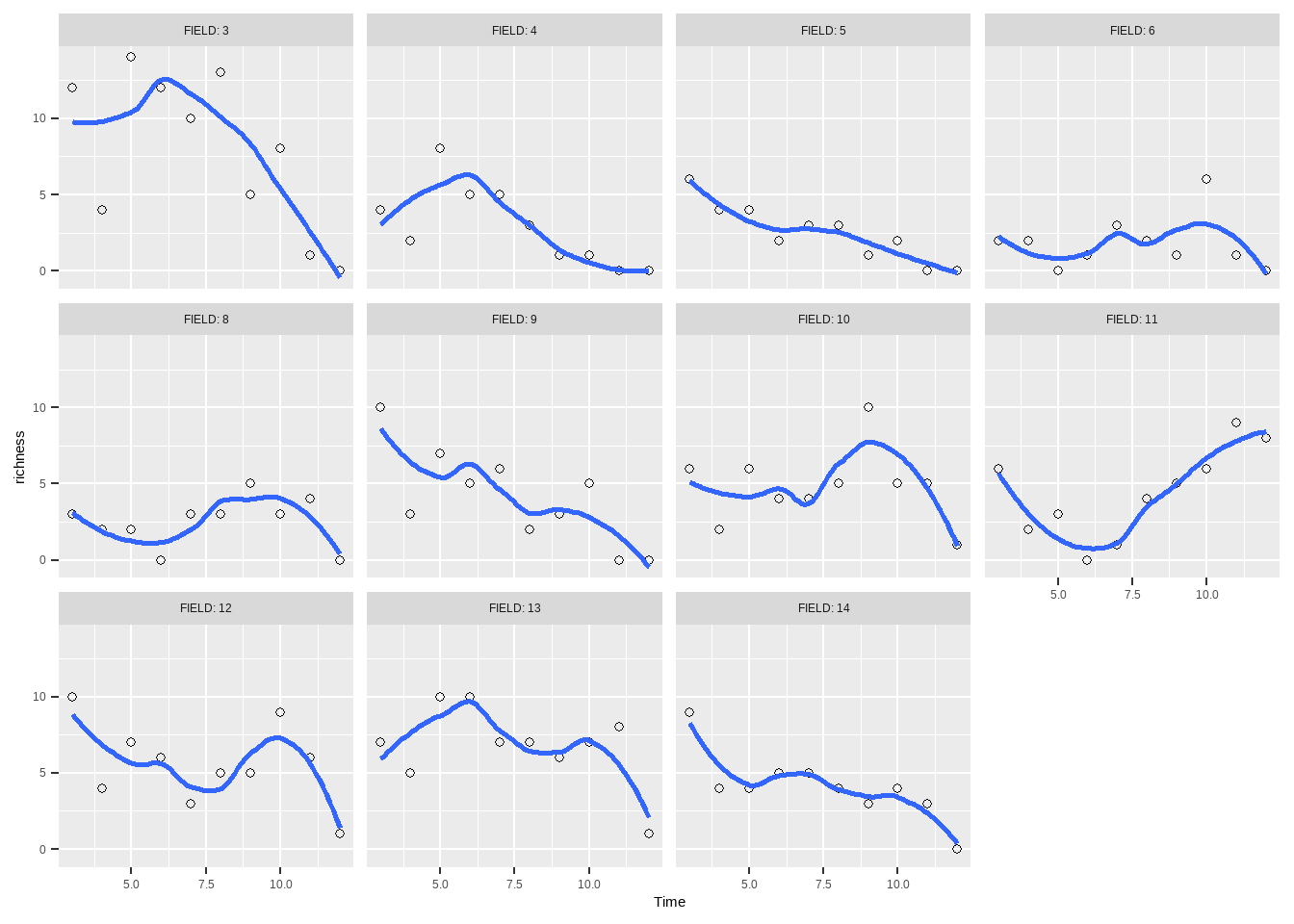
) -> rfb ggplot ( rfb , aes ( Time , richness ) ) + geom_point ( pch = 21 ) +
geom_smooth ( method = "loess" , se = F ) +
facet_wrap ( vars ( FIELD ) , labeller = "label_both" )
Show the code owls <- read_delim ( "data/AED/Owls.txt" ) owls |> mutate ( NCalls = SiblingNegotiation , log_broodsize = log ( BroodSize ) , ) ->
owls
Show the code de <- read_delim ( "data/AED/DeerEcervi.txt" ) de |> mutate (
Ecervi_binary = if_else ( Ecervi > 0 , 1 , Ecervi ) ,
Sex = factor ( Sex ) ,
Length_center = scale ( Length , center = T , scale = F ) ,
) -> de
gee
https://www.statsmodels.org/stable//gee.html
Show the code library ( nlme ) Oxboys |> head ( n= 18 ) #> Grouped Data: height ~ age | Subject #> Subject age height Occasion #> 1 1 -1.0000 140.5 1 #> 2 1 -0.7479 143.4 2 #> 3 1 -0.4630 144.8 3 #> 4 1 -0.1643 147.1 4 #> 5 1 -0.0027 147.7 5 #> 6 1 0.2466 150.2 6 #> 7 1 0.5562 151.7 7 #> 8 1 0.7781 153.3 8 #> 9 1 0.9945 155.8 9 #> 10 2 -1.0000 136.9 1 #> 11 2 -0.7479 139.1 2 #> 12 2 -0.4630 140.1 3 #> 13 2 -0.1643 142.6 4 #> 14 2 -0.0027 143.2 5 #> 15 2 0.2466 144.0 6 #> 16 2 0.5562 145.8 7 #> 17 2 0.7781 146.8 8 #> 18 2 0.9945 148.3 9 df_long <- Oxboys
Show the code library ( gee ) g1 <- gee ( height ~ age ,data = df_long ,id = Subject ,corstr = "AR-M" ,Mv = 1 ) #> (Intercept) age #> 149.371801 6.521022 g1 #> #> GEE: GENERALIZED LINEAR MODELS FOR DEPENDENT DATA #> gee S-function, version 4.13 modified 98/01/27 (1998) #> #> Model: #> Link: Identity #> Variance to Mean Relation: Gaussian #> Correlation Structure: AR-M , M = 1 #> #> Call: #> gee(formula = height ~ age, id = Subject, data = df_long, corstr = "AR-M", #> Mv = 1) #> #> Number of observations : 234 #> #> Maximum cluster size : 9 #> #> #> Coefficients: #> (Intercept) age #> 149.719096 6.547328 #> #> Estimated Scale Parameter: 65.41743 #> Number of Iterations: 2 #> #> Working Correlation[1:4,1:4] #> [,1] [,2] [,3] [,4] #> [1,] 1.0000000 0.9892949 0.9787045 0.9682274 #> [2,] 0.9892949 1.0000000 0.9892949 0.9787045 #> [3,] 0.9787045 0.9892949 1.0000000 0.9892949 #> [4,] 0.9682274 0.9787045 0.9892949 1.0000000 #> #> #> Returned Error Value: #> [1] 0 summary ( g1 ) #> #> GEE: GENERALIZED LINEAR MODELS FOR DEPENDENT DATA #> gee S-function, version 4.13 modified 98/01/27 (1998) #> #> Model: #> Link: Identity #> Variance to Mean Relation: Gaussian #> Correlation Structure: AR-M , M = 1 #> #> Call: #> gee(formula = height ~ age, id = Subject, data = df_long, corstr = "AR-M", #> Mv = 1) #> #> Summary of Residuals: #> Min 1Q Median 3Q Max #> -22.0304139 -5.4912438 0.1324571 4.3822174 18.5695861 #> #> #> Coefficients: #> Estimate Naive S.E. Naive z Robust S.E. Robust z #> (Intercept) 149.719096 1.5531285 96.39840 1.5847569 94.47449 #> age 6.547328 0.3177873 20.60286 0.3042478 21.51972 #> #> Estimated Scale Parameter: 65.41743 #> Number of Iterations: 2 #> #> Working Correlation #> [,1] [,2] [,3] [,4] [,5] [,6] [,7] #> [1,] 1.0000000 0.9892949 0.9787045 0.9682274 0.9578625 0.9476085 0.9374643 #> [2,] 0.9892949 1.0000000 0.9892949 0.9787045 0.9682274 0.9578625 0.9476085 #> [3,] 0.9787045 0.9892949 1.0000000 0.9892949 0.9787045 0.9682274 0.9578625 #> [4,] 0.9682274 0.9787045 0.9892949 1.0000000 0.9892949 0.9787045 0.9682274 #> [5,] 0.9578625 0.9682274 0.9787045 0.9892949 1.0000000 0.9892949 0.9787045 #> [6,] 0.9476085 0.9578625 0.9682274 0.9787045 0.9892949 1.0000000 0.9892949 #> [7,] 0.9374643 0.9476085 0.9578625 0.9682274 0.9787045 0.9892949 1.0000000 #> [8,] 0.9274287 0.9374643 0.9476085 0.9578625 0.9682274 0.9787045 0.9892949 #> [9,] 0.9175005 0.9274287 0.9374643 0.9476085 0.9578625 0.9682274 0.9787045 #> [,8] [,9] #> [1,] 0.9274287 0.9175005 #> [2,] 0.9374643 0.9274287 #> [3,] 0.9476085 0.9374643 #> [4,] 0.9578625 0.9476085 #> [5,] 0.9682274 0.9578625 #> [6,] 0.9787045 0.9682274 #> [7,] 0.9892949 0.9787045 #> [8,] 1.0000000 0.9892949 #> [9,] 0.9892949 1.0000000 data ( epil ,package = "MASS" ) gee1 <- gee ( y ~ age + trt + base ,id= subject ,data = epil ,family = poisson ,corstr = "exchangeable" ) #> (Intercept) age trtprogabide base #> 0.57304359 0.02234757 -0.15188049 0.02263524 summary ( gee1 ) #> #> GEE: GENERALIZED LINEAR MODELS FOR DEPENDENT DATA #> gee S-function, version 4.13 modified 98/01/27 (1998) #> #> Model: #> Link: Logarithm #> Variance to Mean Relation: Poisson #> Correlation Structure: Exchangeable #> #> Call: #> gee(formula = y ~ age + trt + base, id = subject, data = epil, #> family = poisson, corstr = "exchangeable") #> #> Summary of Residuals: #> Min 1Q Median 3Q Max #> -15.742906 -3.318756 -1.186874 1.295122 63.957902 #> #> #> Coefficients: #> Estimate Naive S.E. Naive z Robust S.E. Robust z #> (Intercept) 0.57304359 0.451797966 1.268362 0.360726141 1.5885835 #> age 0.02234757 0.013412798 1.666138 0.011400956 1.9601489 #> trtprogabide -0.15188049 0.159304397 -0.953398 0.171051111 -0.8879246 #> base 0.02263524 0.001696439 13.342795 0.001226748 18.4514092 #> #> Estimated Scale Parameter: 5.087384 #> Number of Iterations: 1 #> #> Working Correlation #> [,1] [,2] [,3] [,4] #> [1,] 1.0000000 0.3933815 0.3933815 0.3933815 #> [2,] 0.3933815 1.0000000 0.3933815 0.3933815 #> [3,] 0.3933815 0.3933815 1.0000000 0.3933815 #> [4,] 0.3933815 0.3933815 0.3933815 1.0000000
geepack
Show the code library ( geepack ) rfb_gee <- geeglm ( richness ~ offset ( log_AREA ) + SPTREAT + DEPTH + DEPTH2 , family = poisson ( link = "log" ) ,
data = rfb ,
id= FIELD ,
corstr = "ar1" )
summary ( rfb_gee ) #> #> Call: #> geeglm(formula = richness ~ offset(log_AREA) + SPTREAT + DEPTH + #> DEPTH2, family = poisson(link = "log"), data = rfb, id = FIELD, #> corstr = "ar1") #> #> Coefficients: #> Estimate Std.err Wald Pr(>|W|) #> (Intercept) -0.6782034 0.2610088 6.752 0.00937 ** #> SPTREATrlfld -0.5223137 0.2287644 5.213 0.02242 * #> DEPTH 0.0498238 0.0193149 6.654 0.00989 ** #> DEPTH2 -0.0011411 0.0004908 5.406 0.02007 * #> --- #> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 #> #> Correlation structure = ar1 #> Estimated Scale Parameters: #> #> Estimate Std.err #> (Intercept) 2.334 0.2927 #> Link = identity #> #> Estimated Correlation Parameters: #> Estimate Std.err #> alpha 0.4215 0.09034 #> Number of clusters: 11 Maximum cluster size: 10 rfb_gee2 <- geeglm ( richness ~ offset ( log_AREA ) + SPTREAT , family = poisson ( link = "log" ) ,
data = rfb ,
id= FIELD ,
corstr = "ar1" )
# Wald's Test anova ( rfb_gee ,rfb_gee2 ) #> Analysis of 'Wald statistic' Table #> #> Model 1 richness ~ offset(log_AREA) + SPTREAT + DEPTH + DEPTH2 #> Model 2 richness ~ offset(log_AREA) + SPTREAT #> Df X2 P(>|Chi|) #> 1 2 6.88 0.032 * #> --- #> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
\[
E(Y_{is})=\mu_{is}=e^{-0.678+0.0498×DEPTH-0.001×DEPTH^2-0.522×SPTREAT_{is}}\\
var(Y_{is})= 2.33 × \mu_{is} \\
cor(Y_{is},Y_{it})=0.422^{|s-t|}
\]
作业相关矩阵 corstr ,比较QIC,一般越小越好。
Show the code QIC ( rfb_gee ) #> QIC QICu Quasi Lik CIC params QICC #> -467.536 -471.921 239.961 6.193 4.000 -455.536 QIC ( rfb_gee2 ) #> QIC QICu Quasi Lik CIC params QICC #> -451.065 -457.436 230.718 5.185 2.000 -447.637
GLM 连接函数
GLM的形式如下:
\[ g(\mu_{ij})=\beta_0+\beta_1x_{ij_1}+\beta_2x_{ij_2}+...+\beta_px_{ij_p} \]
其中,g() 是一个连接函数,用于将自变量的线性组合与因变量的均值联系起来。常见的连接函数包括恒等连接函数(identity)、logistic连接函数(logit)、逆正弦连接函数(inverse sine)函数等。i 表示观测对象的索引,j 表示时间点或相关性结构的索引,uij 表示因变量的均值,β 表示待估计的系数,Xij 表示自变量。
\[
\eta = \beta \mathbf{X}+ \alpha
\]
\[
E(y)=g^{-1}(\eta)
\]
对于计数数据:
\[
E(y)=e^{\eta}=e^{\beta \mathbf{X} +\alpha}, 此时g(\mu)=\ln(\mu)=\mathbf{X}\beta
\]
Show the code rfb_glm <- glm ( richness ~ offset ( log_AREA ) + SPTREAT + DEPTH + DEPTH2 , family = quasipoisson ( link = "log" ) ,
data = rfb )
owls_glm <- glm ( NCalls ~ offset ( log_broodsize ) + SexParent * FoodTreatment + SexParent *
ArrivalTime ,
family = poisson ( link = "log" ) ,
data = owls
)
对于二分类数据:
\[
E(y)=\frac{e^{\beta \mathbf{X} +\alpha}}{1+e^{\beta\mathbf{X}+\alpha}}, 此时g(\mu)=\ln(\frac{\mu}{1-\mu})=logit(\mu)
\]
Show the code de_glm <- glm ( Ecervi_binary ~ Length_center * Sex , family = binomial ( link = "logit" ) ,
data = de )
summary ( de_glm ) #> #> Call: #> glm(formula = Ecervi_binary ~ Length_center * Sex, family = binomial(link = "logit"), #> data = de) #> #> Coefficients: #> Estimate Std. Error z value Pr(>|z|) #> (Intercept) 0.65241 0.10960 5.95 2.6e-09 *** #> Length_center 0.02511 0.00558 4.50 6.7e-06 *** #> Sex2 0.16387 0.17423 0.94 0.347 #> Length_center:Sex2 0.02011 0.00972 2.07 0.039 * #> --- #> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 #> #> (Dispersion parameter for binomial family taken to be 1) #> #> Null deviance: 1073.1 on 825 degrees of freedom #> Residual deviance: 1003.7 on 822 degrees of freedom #> AIC: 1012 #> #> Number of Fisher Scoring iterations: 4
方差
\[
var(Y_{is}|X_{is})=\Phi × \nu(\mu_{is})
\]
其中,Φ 是scale parameter (overdispersion),v() 是方差函数。
相关性结构
R(α) (working correlation)
非结构化相关:cor(Yis ,Yit )=αst
自回归相关:cor(Yis ,Yit )=α|s-t|
exchangeable 等相关:cor(Yis ,Yit )=α
independence,独立,cor(Yis ,Yit )=I
GEE
GLM的期望和方差:
\[ E(Y_{ij})=b'(\theta_{ij})\\ Var(Y_{ij})=b''(\theta_{ij})\ \Phi \]
假定潜在的随机成分Vi :
\[
V_i=A_i^{1/2}R(\alpha)A_i^{1/2}\ \Phi
\]
其中,Ai =diag(b''(θi1),...,b''(θij)) 。
GEE的形式如下:
\[
U(\beta)=\sum_{i=1}^{n} D'_iV_i^{-1}(y_i-\mu_i)=0
\]
其中,$U(β) $是一个包含待估计参数的函数,quasi-deviance \(D'_i = \left(\frac{\partial \mu_i}{\partial \beta}\right)'\) ,\(V_i\) 是方差-协方差矩阵,\(R(\alpha)\) 是相关性结构矩阵,y 是观测数据,μ 是模型的均值预测值。采用迭代重复加权最小二乘法(iteratively reweighted least squares ,IWLS)),偏微分方程估计参数。