14 线性混合效应模型

Modified

November 20, 2024

线性混合效应模型（Linear Mixed-effect Model，LMM）用于分析具有固定效应和随机效应的数据结构。它能够处理数据中的个体异质性和组内相关性。如果数据满足正态分布但有组内相关性，使用线性混合效应模型。

LMM可以采用多种相关性假设：

unstructured
homogeneous toeplitz
auto-regression AR(1)
homogeneous auto-regression ARH(1)
compound symmetry
homogeneous compound symmetry

对于连续数据，mixed model repeated measures（MMRM）

对于分类数据或计数数据，generalized linear mixed-effects model(GLMM)

Mixed Effects Models and Extensions in Ecology with R 第5章

线性混合模型的一般表达形式：

\[ Y = \mathbf{X} \beta + \mathbf{Z} \gamma + \epsilon \]

其中：

$\mathbf{X}$是固定效应自变量矩阵。
$\beta$ 是固定效应的回归系数。
$\mathbf{Z}$ 是随机效应自变量矩阵。
$\gamma$ 是随机效应的回归系数。
$\epsilon$ 是误差项。

固定效应是感兴趣的自变量，表示所有个体都相同的效应

随机效应：随机截距表示不同个体的基线差异，随机斜率表示不同个体对自变量的响应差异。

14.1 `lme4::lmer()`

lmer() 的表达式如下：

\[ lmer (data,formual= DV \sim Fixed\_Factor + \\ (Random\_intercept + Random\_slope | Random\_Factor)+\$Random\_intercept + Random\_slope | Random\_Factor)+... \$ \]

截距中，1表示随机截距，0表示固定截距，默认截距为1。

LME	表达式	简写
随机截距+随机斜率	y~x+( 1+x \| id )	y~x+( x \| id )
随机截距+固定斜率	y~x+( 1+1 \| id )	y~x+( 1 \| id )
固定截距+随机斜率	y~x+( 0+x \| id )	NA
线性模型：固定截距+固定斜率	y~x	NA

Show the code

rikz <- read_delim("data/AED/RIKZ.txt")
rikz <- rikz %>% 
    mutate(
        Beach = factor(Beach),
        Exposure = factor(Exposure)
    )
head(rikz)
#> # A tibble: 6 × 5
#>   Sample Richness Exposure    NAP Beach
#>    <dbl>    <dbl> <fct>     <dbl> <fct>
#> 1      1       11 10        0.045 1    
#> 2      2       10 10       -1.04  1    
#> 3      3       13 10       -1.34  1    
#> 4      4       11 10        0.616 1    
#> 5      5       10 10       -0.684 1    
#> 6      6        8 8         1.19  2

14.2 随机截距+随机斜率

\[ \eta_{(nrow \times 1)} = \mathbf{X}_{nrow \times 1} \beta_{1 \times 1} + \mathbf{Z}_{nrow \times 2n_{subjects}} \mathbf{\gamma}_{2n_{subjects} \times 1} + \epsilon_i \]

Z有两倍于受试者数量的列，每个受试者的随机截距和随机斜率

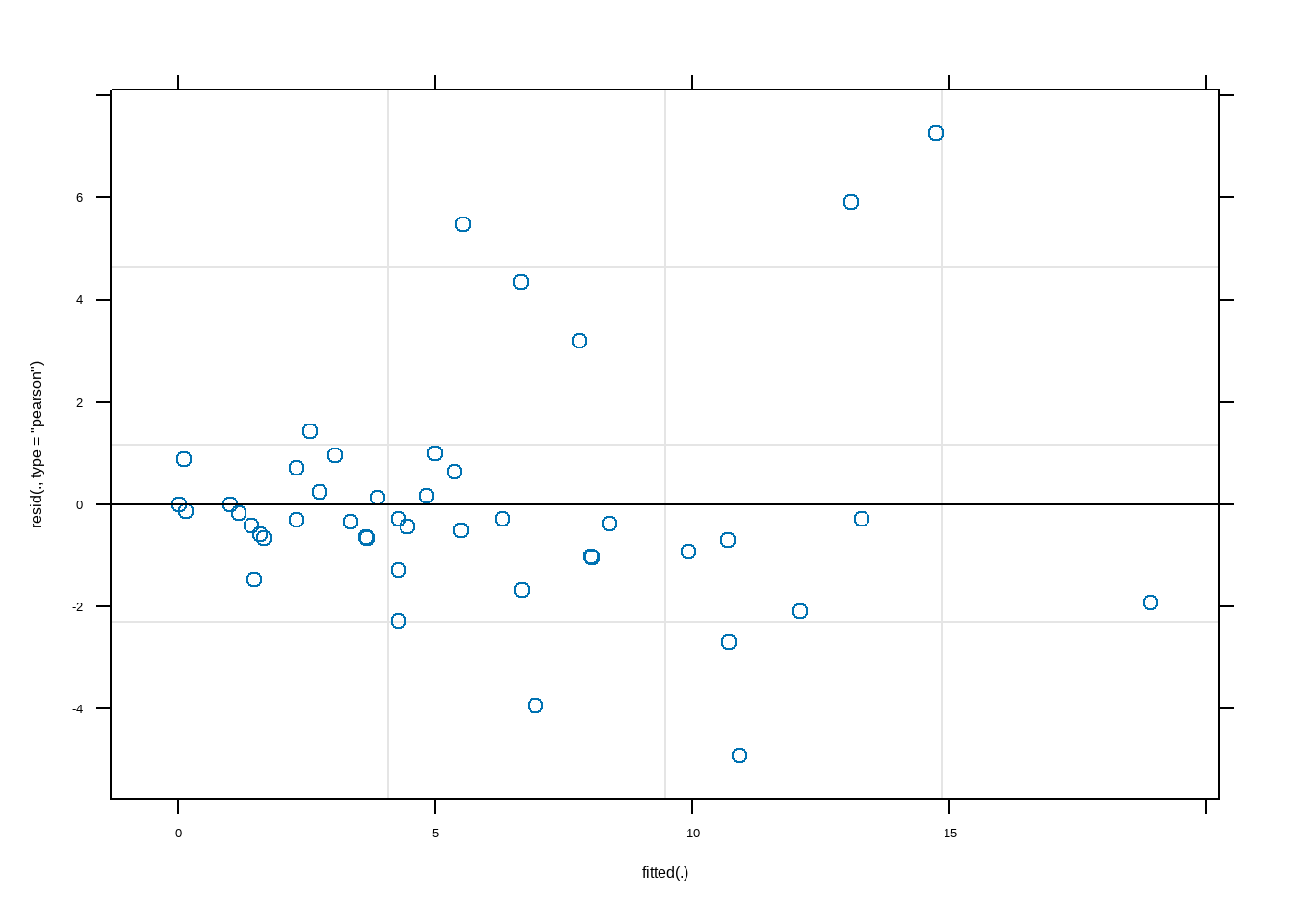
Show the code

library(lmerTest)
conflicted::conflicts_prefer(lmerTest::lmer)
lme1 <- lmer(Richness ~ 1 + NAP + Exposure+ NAP:Exposure + (1 + NAP |Beach) ,data = rikz)
summary(lme1)
#> Linear mixed model fit by REML. t-tests use Satterthwaite's method [
#> lmerModLmerTest]
#> Formula: Richness ~ 1 + NAP + Exposure + NAP:Exposure + (1 + NAP | Beach)
#>    Data: rikz
#> 
#> REML criterion at convergence: 207.2
#> 
#> Scaled residuals: 
#>      Min       1Q   Median       3Q      Max 
#> -1.92384 -0.36066 -0.13343  0.09819  2.84228 
#> 
#> Random effects:
#>  Groups   Name        Variance Std.Dev. Corr 
#>  Beach    (Intercept) 3.758    1.938         
#>           NAP         2.837    1.684    -1.00
#>  Residual             6.535    2.556         
#> Number of obs: 45, groups:  Beach, 9
#> 
#> Fixed effects:
#>                Estimate Std. Error      df t value Pr(>|t|)   
#> (Intercept)     13.3457     2.2784  5.0864   5.858  0.00194 **
#> NAP             -4.1753     2.1243  5.7080  -1.965  0.09942 . 
#> Exposure10      -5.3273     2.5556  5.1415  -2.085  0.09000 . 
#> Exposure11      -9.7660     2.5653  5.1903  -3.807  0.01169 * 
#> NAP:Exposure10   0.1646     2.3621  5.5602   0.070  0.94688   
#> NAP:Exposure11   2.7273     2.3715  5.6329   1.150  0.29661   
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Correlation of Fixed Effects:
#>             (Intr) NAP    Exps10 Exps11 NAP:E10
#> NAP         -0.770                             
#> Exposure10  -0.892  0.686                      
#> Exposure11  -0.888  0.683  0.792               
#> NAP:Expsr10  0.692 -0.899 -0.775 -0.615        
#> NAP:Expsr11  0.689 -0.896 -0.615 -0.779  0.806 
#> optimizer (nloptwrap) convergence code: 0 (OK)
#> boundary (singular) fit: see help('isSingular')



plot(lme1)

Show the code


AIC(lme1)
#> [1] 227.1558
BIC(lme1)
#> [1] 245.2224
logLik(lme1)
#> 'log Lik.' -103.5779 (df=10)

# library(broom.mixed)
# tidy(lme1)


library(nlme)
lme(Richness ~ 1 + NAP * Exposure,
             random = ~ 1 + NAP | Beach ,
             data = rikz,
             control = lmeControl(opt = "optim", 
                                  msMaxIter = 1000, 
                                  msMaxEval = 5000)
    ) %>% 
    summary()
#> Linear mixed-effects model fit by REML
#>   Data: rikz 
#>        AIC      BIC    logLik
#>   227.2046 243.8402 -103.6023
#> 
#> Random effects:
#>  Formula: ~1 + NAP | Beach
#>  Structure: General positive-definite, Log-Cholesky parametrization
#>             StdDev   Corr  
#> (Intercept) 1.939709 (Intr)
#> NAP         1.689580 -0.996
#> Residual    2.554676       
#> 
#> Fixed effects:  Richness ~ 1 + NAP * Exposure 
#>                    Value Std.Error DF   t-value p-value
#> (Intercept)    13.345694  2.278989 33  5.855970  0.0000
#> NAP            -4.175271  2.128084 33 -1.961986  0.0582
#> Exposure10     -5.323695  2.556406  6 -2.082492  0.0825
#> Exposure11     -9.765613  2.566035  6 -3.805720  0.0089
#> NAP:Exposure10  0.167146  2.366467 33  0.070631  0.9441
#> NAP:Exposure11  2.726865  2.375786 33  1.147774  0.2593
#>  Correlation: 
#>                (Intr) NAP    Exps10 Exps11 NAP:E10
#> NAP            -0.767                             
#> Exposure10     -0.891  0.684                      
#> Exposure11     -0.888  0.682  0.792               
#> NAP:Exposure10  0.690 -0.899 -0.772 -0.613        
#> NAP:Exposure11  0.687 -0.896 -0.613 -0.777  0.806 
#> 
#> Standardized Within-Group Residuals:
#>        Min         Q1        Med         Q3        Max 
#> -1.9251786 -0.3608959 -0.1327685  0.0992999  2.8420571 
#> 
#> Number of Observations: 45
#> Number of Groups: 9

这个模型的公式可以分解为：

REML 限制性最大似然准则 207.2，评估模型的拟合优度
Scaled residuals
随机效应部分：Beach 作为随机效应的分组变量，包含随机截距和随机斜率（NAP），相关性为 -1，说明随机截距和随机斜率之间呈现完全负相关关系。
固定效应部分：Richness 的预测由截距、NAP（数值变量）和 Exposure（分类变量，包含 Exposure10 和 Exposure11）及其交互项构成。
固定效应的相关性矩阵

Show the code

# 标准化模型残差分布
quantile(residuals(lme1,type="pearson",scaled=T))
#>         0%        25%        50%        75%       100% 
#> -1.9238372 -0.3606612 -0.1334336  0.0981939  2.8422803
# 查看固定效应和显著性检验
fixef(lme1)   
#>    (Intercept)            NAP     Exposure10     Exposure11 NAP:Exposure10 
#>     13.3456944     -4.1752712     -5.3272654     -9.7660482      0.1646123 
#> NAP:Exposure11 
#>      2.7273068
anova(lme1)
#> Type III Analysis of Variance Table with Satterthwaite's method
#>               Sum Sq Mean Sq NumDF  DenDF F value  Pr(>F)  
#> NAP           90.646  90.646     1 5.5230 13.8711 0.01139 *
#> Exposure     109.852  54.926     2 5.2975  8.4051 0.02273 *
#> NAP:Exposure  22.308  11.154     2 5.3880  1.7068 0.26657  
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1


# 随机效应：随机截距和随机斜率  # 每个组的随机截距表示该组的平均值与模型整体平均值（截距）的差异
ranef(lme1) 
#> $Beach
#>     (Intercept)           NAP
#> 1 -4.274356e-02  3.713708e-02
#> 2 -2.709479e-14  2.354089e-14
#> 3  3.819348e-03 -3.318381e-03
#> 4 -2.741786e-01  2.382158e-01
#> 5  3.269522e+00 -2.840673e+00
#> 6  2.736093e-01 -2.377212e-01
#> 7 -3.250033e-03  2.823741e-03
#> 8 -2.148947e+00  1.867079e+00
#> 9 -1.077831e+00  9.364564e-01
#> 
#> with conditional variances for "Beach"
# 随机效应的显著性检验
lmerTest::ranova(lme1)
#> ANOVA-like table for random-effects: Single term deletions
#> 
#> Model:
#> Richness ~ NAP + Exposure + (1 + NAP | Beach) + NAP:Exposure
#>                          npar  logLik    AIC    LRT Df Pr(>Chisq)
#> <none>                     10 -103.58 227.16                     
#> NAP in (1 + NAP | Beach)    8 -105.67 227.35 4.1935  2     0.1229

cor(ranef(lme1)$Beach)
#>             (Intercept) NAP
#> (Intercept)           1  -1
#> NAP                  -1   1

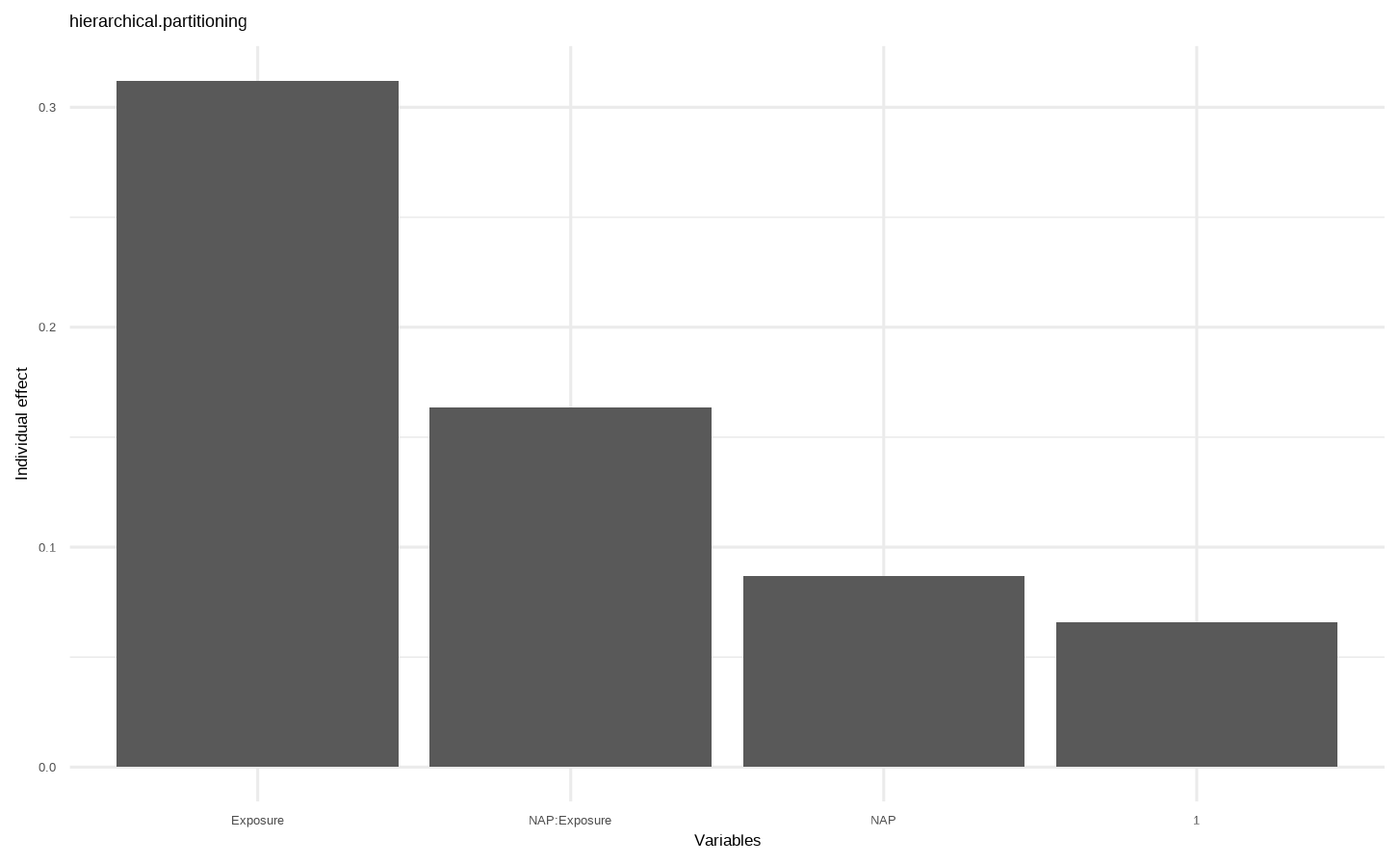
Show the code

e <- glmm.hp::glmm.hp(lme1)
save(e,file = "data/glmm.hp.Rdata")

# $r.squaredGLMM
#            R2m       R2c
# [1,] 0.6279508 0.7811086
# 
# $hierarchical.partitioning
#              Unique Average.share Individual I.perc(%)
# 1            0.0000        0.0657     0.0657     10.46
# NAP          0.0000        0.0867     0.0867     13.81
# Exposure     0.2987        0.0135     0.3122     49.71
# NAP:Exposure 0.0884        0.0750     0.1634     26.02
# 
# $variables
# [1] "1"            "NAP"          "Exposure"     "NAP:Exposure"
# 
# $type
# [1] "hierarchical.partitioning"
# 
# attr(,"class")
# [1] "glmmhp"

Show the code

load("data/glmm.hp.Rdata")
e
#> $r.squaredGLMM
#>            R2m       R2c
#> [1,] 0.6279508 0.7811086
#> 
#> $hierarchical.partitioning
#>              Unique Average.share Individual I.perc(%)
#> 1            0.0000        0.0657     0.0657     10.46
#> NAP          0.0000        0.0867     0.0867     13.81
#> Exposure     0.2987        0.0135     0.3122     49.71
#> NAP:Exposure 0.0884        0.0750     0.1634     26.02
#> 
#> $variables
#> [1] "1"            "NAP"          "Exposure"     "NAP:Exposure"
#> 
#> $type
#> [1] "hierarchical.partitioning"
#> 
#> attr(,"class")
#> [1] "glmmhp"

$r.squaredGLMM

这里呈现了两个衡量模型拟合优度的指标，R2m 和 R2c，分别对应不同的广义决定系数计算方式。
- R2m 的值为 0.6279508，表示固定效应变量解释了大约62.80%的响应变量的方差
- R2c 的值为 0.7811086，表示固定效应和随机效应共同解释了大约78.11%的响应变量的方差

$hierarchical.partitioning

“Unique” 列：展示了各变量独自解释的方差比例
“Average.share” 列：变量与其他变量所有组合的方差解释比例
“Individual” 列：“Unique”和“Average.share”的和，即变量的总贡献
“I.perc (%)” 列：每个变量的相对重要性程度。

$variables

简单列出了模型中涉及的变量名称，这里有 "1"（代表整体截距）、"NAP"、"Exposure" 以及它们的交互项 "NAP:Exposure"，明确了模型在分析中考虑的因素构成。

$type

指出了当前分析结果呈现的类型是 "hierarchical.partitioning"，说明后续如果进一步拓展分析或者对比不同模型等操作时，可以清楚知道这部分结果对应的分析类别。

Show the code

plot(e)

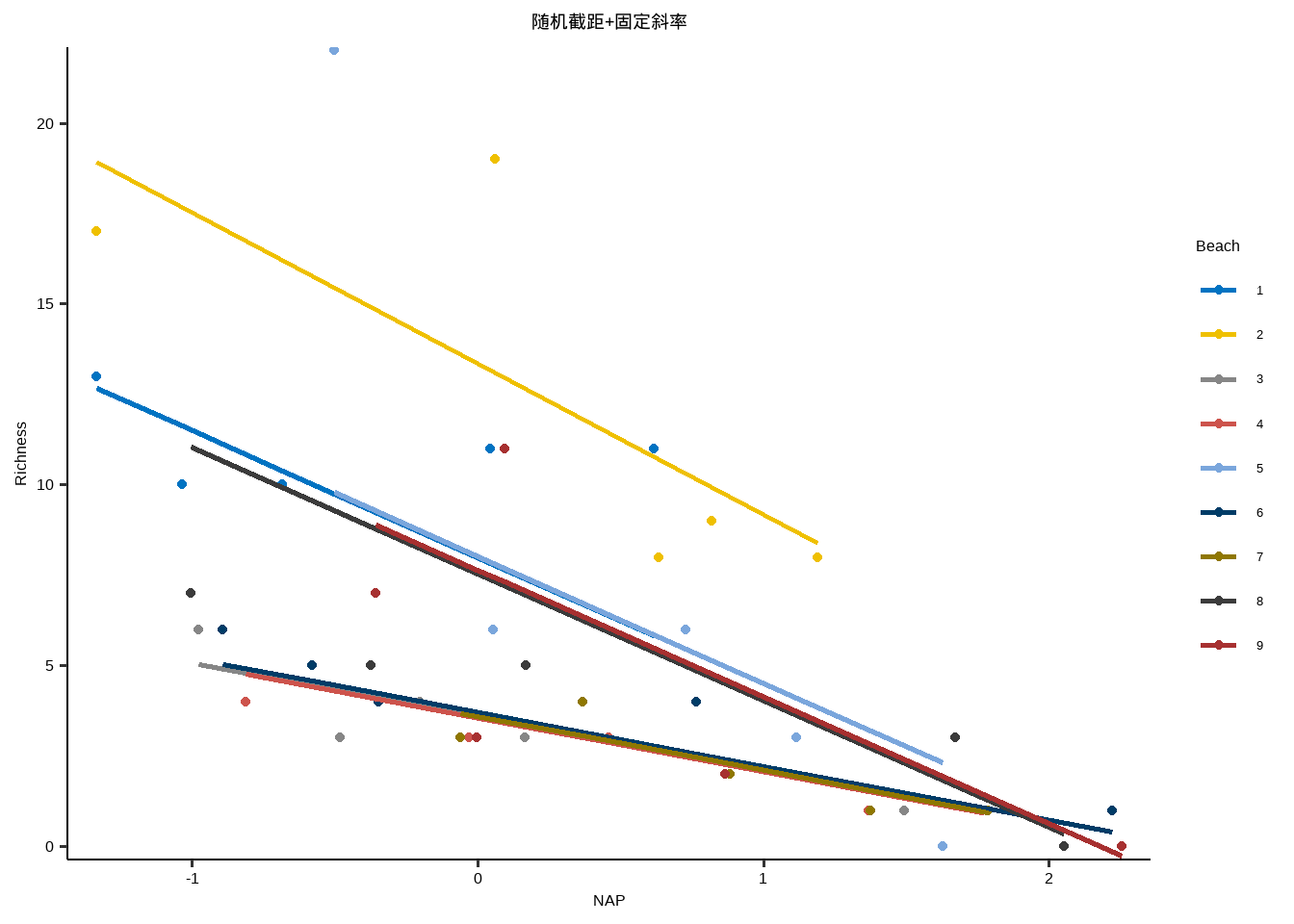
14.3 随机截距+固定斜率

\[ \eta_{(nrow \ \times 1)}=\mathbf{X_{nrow×1}}\beta_{1\times1} +Z_{nrow\times n_{subjects}} \mathbf{\gamma}_{n_{subjects}\times 1}+\epsilon_i \]

Z有一倍于受试者数量的列，每个受试者的随机截距。

Show the code

lme2 <- lmer(Richness ~ 1 + NAP * Exposure+ (1+1 |Beach) ,data = rikz)
summary(lme2)
#> Linear mixed model fit by REML. t-tests use Satterthwaite's method [
#> lmerModLmerTest]
#> Formula: Richness ~ 1 + NAP * Exposure + (1 + 1 | Beach)
#>    Data: rikz
#> 
#> REML criterion at convergence: 211.3
#> 
#> Scaled residuals: 
#>     Min      1Q  Median      3Q     Max 
#> -1.5653 -0.4387 -0.1165  0.1783  4.1098 
#> 
#> Random effects:
#>  Groups   Name        Variance Std.Dev.
#>  Beach    (Intercept) 0.2641   0.5139  
#>  Residual             8.8316   2.9718  
#> Number of obs: 45, groups:  Beach, 9
#> 
#> Fixed effects:
#>                Estimate Std. Error      df t value Pr(>|t|)    
#> (Intercept)     13.3457     1.4836  6.5050   8.996 6.63e-05 ***
#> NAP             -4.1753     1.5051 33.0857  -2.774 0.009030 ** 
#> Exposure10      -5.5450     1.6577  6.4545  -3.345 0.013909 *  
#> Exposure11      -9.7306     1.6705  6.6476  -5.825 0.000781 ***
#> NAP:Exposure10   0.6717     1.6439 34.9341   0.409 0.685306    
#> NAP:Exposure11   2.6888     1.6567 34.2669   1.623 0.113766    
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Correlation of Fixed Effects:
#>             (Intr) NAP    Exps10 Exps11 NAP:E10
#> NAP         -0.278                             
#> Exposure10  -0.895  0.249                      
#> Exposure11  -0.888  0.247  0.795               
#> NAP:Expsr10  0.255 -0.916 -0.276 -0.226        
#> NAP:Expsr11  0.253 -0.908 -0.226 -0.296  0.832
AIC(lme2)
#> [1] 227.3493
BIC(lme2)
#> [1] 241.8026
logLik(lme2)
#> 'log Lik.' -105.6747 (df=8)

2*(1-pt(6.007,35,lower.tail = T))
#> [1] 7.558855e-07



lme(Richness ~ 1 + NAP * Exposure,random= ~ 1+1 |Beach ,data = rikz) %>% 
    summary()
#> Linear mixed-effects model fit by REML
#>   Data: rikz 
#>        AIC      BIC    logLik
#>   227.3493 240.6578 -105.6747
#> 
#> Random effects:
#>  Formula: ~1 + 1 | Beach
#>         (Intercept) Residual
#> StdDev:   0.5138683 2.971793
#> 
#> Fixed effects:  Richness ~ 1 + NAP * Exposure 
#>                    Value Std.Error DF   t-value p-value
#> (Intercept)    13.345694  1.483557 33  8.995739  0.0000
#> NAP            -4.175271  1.505110 33 -2.774063  0.0090
#> Exposure10     -5.544983  1.657659  6 -3.345069  0.0155
#> Exposure11     -9.730595  1.670518  6 -5.824898  0.0011
#> NAP:Exposure10  0.671731  1.643864 33  0.408629  0.6855
#> NAP:Exposure11  2.688806  1.656743 33  1.622947  0.1141
#>  Correlation: 
#>                (Intr) NAP    Exps10 Exps11 NAP:E10
#> NAP            -0.278                             
#> Exposure10     -0.895  0.249                      
#> Exposure11     -0.888  0.247  0.795               
#> NAP:Exposure10  0.255 -0.916 -0.276 -0.226        
#> NAP:Exposure11  0.253 -0.908 -0.226 -0.296  0.832 
#> 
#> Standardized Within-Group Residuals:
#>        Min         Q1        Med         Q3        Max 
#> -1.5652904 -0.4386841 -0.1164805  0.1783113  4.1098230 
#> 
#> Number of Observations: 45
#> Number of Groups: 9

14.4 固定截距+随机斜率

\[ \eta_{(nrow \times 1)} = \mathbf{X}_{nrow \times 1} \beta_{1 \times 1} + \mathbf{Z}_{nrow \times n_{subjects}} \mathbf{\gamma}_{n_{subjects} \times 1} + \epsilon_i \]

Z 有一倍于受试者数量的列，每个受试者的随机斜率。

Show the code

lme3 <- lmer(Richness ~ 1 +  NAP * Exposure + (0 + NAP |Beach) ,data = rikz)
summary(lme3)
#> Linear mixed model fit by REML. t-tests use Satterthwaite's method [
#> lmerModLmerTest]
#> Formula: Richness ~ 1 + NAP * Exposure + (0 + NAP | Beach)
#>    Data: rikz
#> 
#> REML criterion at convergence: 211.4
#> 
#> Scaled residuals: 
#>     Min      1Q  Median      3Q     Max 
#> -1.6048 -0.4448 -0.1226  0.2322  4.1284 
#> 
#> Random effects:
#>  Groups   Name Variance Std.Dev.
#>  Beach    NAP  0.000    0.000   
#>  Residual      9.024    3.004   
#> Number of obs: 45, groups:  Beach, 9
#> 
#> Fixed effects:
#>                Estimate Std. Error      df t value Pr(>|t|)    
#> (Intercept)     13.3457     1.4068 39.0000   9.486 1.11e-11 ***
#> NAP             -4.1753     1.5214 39.0000  -2.744  0.00912 ** 
#> Exposure10      -5.5318     1.5715 39.0000  -3.520  0.00111 ** 
#> Exposure11      -9.7284     1.5852 39.0000  -6.137 3.34e-07 ***
#> NAP:Exposure10   0.6278     1.6583 39.0000   0.379  0.70703    
#> NAP:Exposure11   2.6835     1.6725 39.0000   1.604  0.11668    
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Correlation of Fixed Effects:
#>             (Intr) NAP    Exps10 Exps11 NAP:E10
#> NAP         -0.297                             
#> Exposure10  -0.895  0.266                      
#> Exposure11  -0.887  0.263  0.794               
#> NAP:Expsr10  0.272 -0.917 -0.294 -0.242        
#> NAP:Expsr11  0.270 -0.910 -0.242 -0.315  0.835 
#> optimizer (nloptwrap) convergence code: 0 (OK)
#> boundary (singular) fit: see help('isSingular')


lme(Richness ~ 1 + NAP * Exposure,random= ~ 0+NAP |Beach ,data = rikz) %>% 
    summary()
#> Linear mixed-effects model fit by REML
#>   Data: rikz 
#>        AIC      BIC    logLik
#>   227.3962 240.7047 -105.6981
#> 
#> Random effects:
#>  Formula: ~0 + NAP | Beach
#>                  NAP Residual
#> StdDev: 0.0001223769 3.004042
#> 
#> Fixed effects:  Richness ~ 1 + NAP * Exposure 
#>                    Value Std.Error DF   t-value p-value
#> (Intercept)    13.345694  1.406821 33  9.486418  0.0000
#> NAP            -4.175271  1.521443 33 -2.744283  0.0097
#> Exposure10     -5.531822  1.571461  6 -3.520178  0.0125
#> Exposure11     -9.728394  1.585241  6 -6.136854  0.0009
#> NAP:Exposure10  0.627847  1.658269 33  0.378616  0.7074
#> NAP:Exposure11  2.683487  1.672531 33  1.604447  0.1181
#>  Correlation: 
#>                (Intr) NAP    Exps10 Exps11 NAP:E10
#> NAP            -0.297                             
#> Exposure10     -0.895  0.266                      
#> Exposure11     -0.887  0.263  0.794               
#> NAP:Exposure10  0.272 -0.917 -0.294 -0.242        
#> NAP:Exposure11  0.270 -0.910 -0.242 -0.315  0.835 
#> 
#> Standardized Within-Group Residuals:
#>        Min         Q1        Med         Q3        Max 
#> -1.6048271 -0.4448474 -0.1225590  0.2321686  4.1283628 
#> 
#> Number of Observations: 45
#> Number of Groups: 9

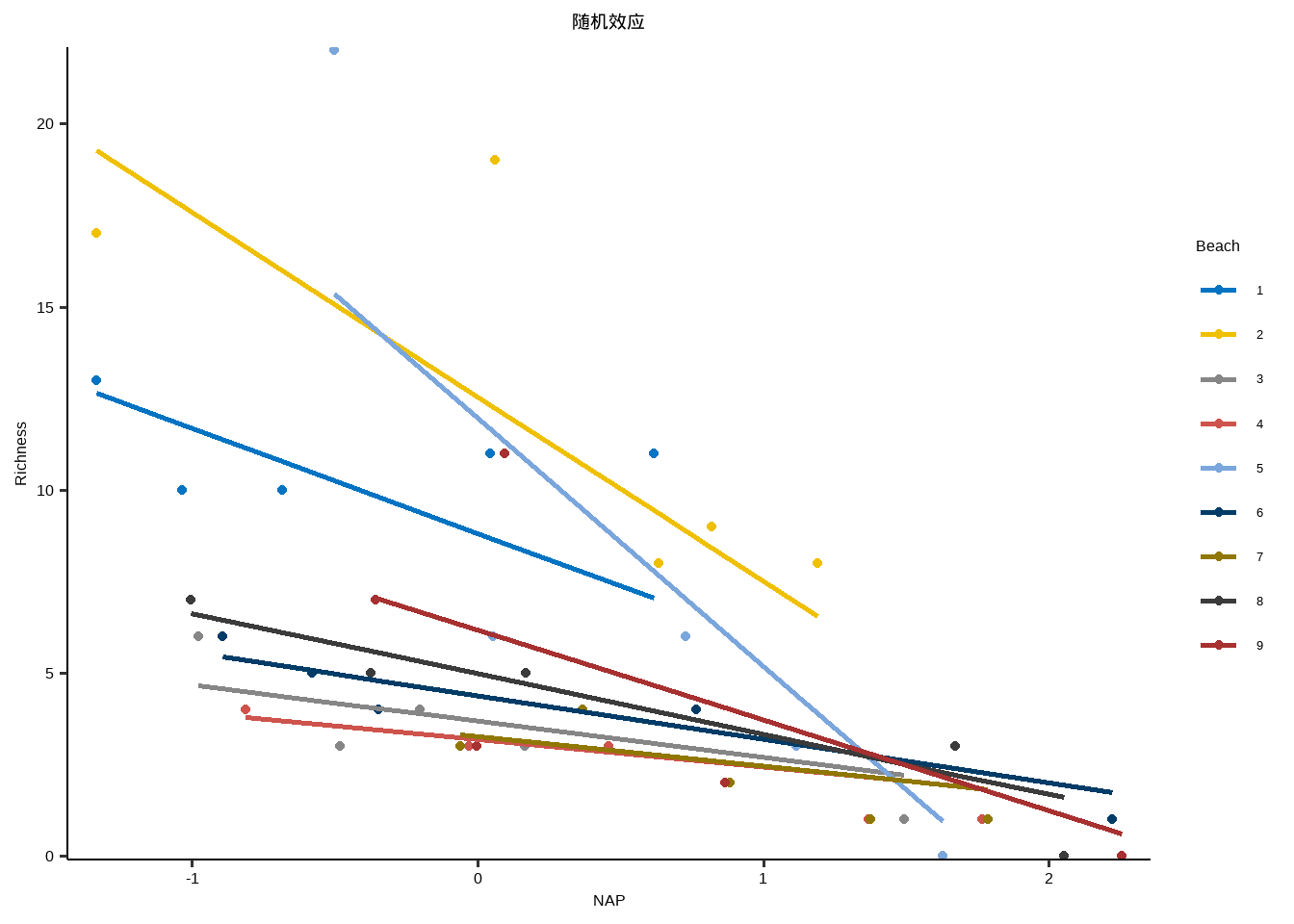
14.5 随机效应模型

Show the code


lme4 <- lmer(Richness ~ 1 + (1+NAP|Beach) ,data = rikz)
summary(lme4)
#> Linear mixed model fit by REML. t-tests use Satterthwaite's method [
#> lmerModLmerTest]
#> Formula: Richness ~ 1 + (1 + NAP | Beach)
#>    Data: rikz
#> 
#> REML criterion at convergence: 242.9
#> 
#> Scaled residuals: 
#>     Min      1Q  Median      3Q     Max 
#> -2.1607 -0.4415 -0.1999  0.2065  2.6133 
#> 
#> Random effects:
#>  Groups   Name        Variance Std.Dev. Corr 
#>  Beach    (Intercept) 28.173   5.308         
#>           NAP         11.292   3.360    -0.95
#>  Residual              6.697   2.588         
#> Number of obs: 45, groups:  Beach, 9
#> 
#> Fixed effects:
#>             Estimate Std. Error     df t value Pr(>|t|)  
#> (Intercept)   2.8023     0.8218 3.7478    3.41   0.0299 *
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

ranef(lme4)
#> $Beach
#>   (Intercept)        NAP
#> 1   6.0112287 -2.8605659
#> 2   9.7420133 -5.0379262
#> 3   0.8792316 -0.9838634
#> 4   0.3721784 -0.7548668
#> 5   9.1546337 -6.7668418
#> 6   1.5719076 -1.1861532
#> 7   0.4484228 -0.7999673
#> 8   2.1690889 -1.6492031
#> 9   3.3610981 -2.4639704
#> 
#> with conditional variances for "Beach"

lme(Richness ~ 1 ,random= ~ 1+NAP |Beach ,data = rikz) %>% 
    summary()
#> Linear mixed-effects model fit by REML
#>   Data: rikz 
#>       AIC      BIC    logLik
#>   252.935 261.8559 -121.4675
#> 
#> Random effects:
#>  Formula: ~1 + NAP | Beach
#>  Structure: General positive-definite, Log-Cholesky parametrization
#>             StdDev   Corr  
#> (Intercept) 5.307778 (Intr)
#> NAP         3.360427 -0.948
#> Residual    2.587870       
#> 
#> Fixed effects:  Richness ~ 1 
#>                Value Std.Error DF  t-value p-value
#> (Intercept) 2.802324 0.8217849 36 3.410046  0.0016
#> 
#> Standardized Within-Group Residuals:
#>        Min         Q1        Med         Q3        Max 
#> -2.1606764 -0.4415215 -0.1998751  0.2064870  2.6133376 
#> 
#> Number of Observations: 45
#> Number of Groups: 9

14.6 线性模型：固定截距+ 固定斜率

Show the code

lm <- lm(Richness ~ 1 + NAP * Exposure ,data = rikz)
lm
#> 
#> Call:
#> lm(formula = Richness ~ 1 + NAP * Exposure, data = rikz)
#> 
#> Coefficients:
#>    (Intercept)             NAP      Exposure10      Exposure11  NAP:Exposure10  
#>        13.3457         -4.1753         -5.5318         -9.7284          0.6278  
#> NAP:Exposure11  
#>         2.6835

14.7 模型选择

限制最大似然法REML

赤池信息准则（AIC）

\[ kIC=−2log(\mathcal{L})+2k\]

其中：
- $\mathcal{L}$ 是似然函数。
- $k$ 是模型参数的数量。
贝叶斯信息准则（BIC）

\[ BIC=−2log(\mathcal{L})+klog(n) \]

其中：
- $n$ 是样本量。

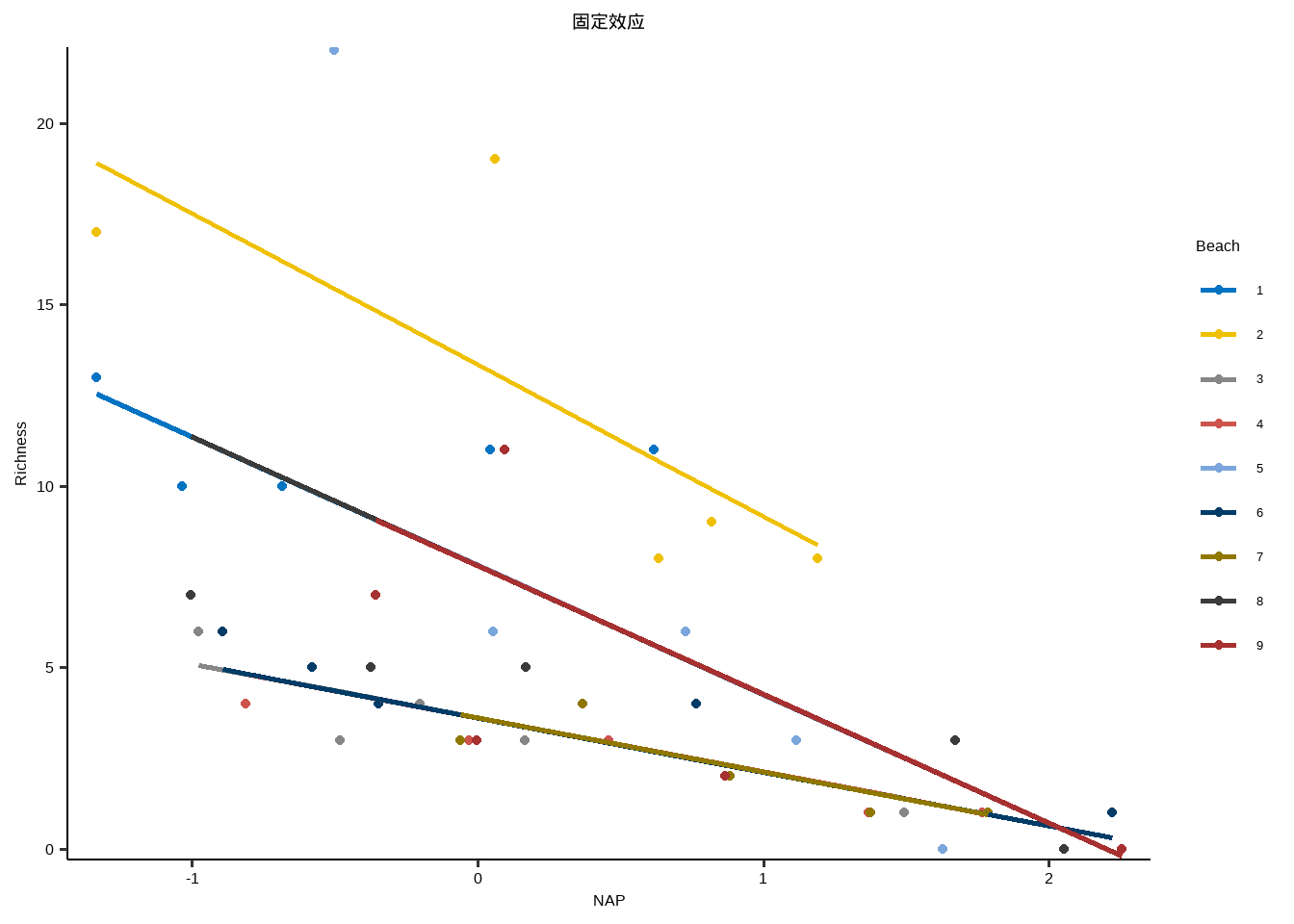
Show the code


plot_lme <- function(model, title) {
    ggplot(rikz, aes(NAP, Richness, group = Beach, color = Beach)) +
        geom_point() +
        geom_line(
            data =  bind_cols(rikz, .pred = predict(model, rikz)),
            mapping = aes(y = .pred),
            linewidth = 1
        ) +
        labs(title = title)+
        scale_x_continuous(expand = (mult=c(0,.1)))+
        scale_y_continuous(expand = (mult=c(0,.1)))+
    ggsci::scale_color_jco() +
        ggpubr::theme_pubr() +
        theme(legend.position = "right",
              plot.title = element_text(hjust = .5))
}


lme_plot <- map2(list(lme1,lme2,lme3, lme4,lm),list("随机截距+随机斜率","随机截距+固定斜率","固定截距+随机斜率","随机效应","固定效应"),plot_lme)


lme_plot
#> [[1]]

#> 
#> [[2]]

#> 
#> [[3]]

#> 
#> [[4]]

#> 
#> [[5]]

Show the code

anova(lme1,lme2,lme3,lme4,lm)
#> Data: rikz
#> Models:
#> lme4: Richness ~ 1 + (1 + NAP | Beach)
#> lm: Richness ~ 1 + NAP * Exposure
#> lme2: Richness ~ 1 + NAP * Exposure + (1 + 1 | Beach)
#> lme3: Richness ~ 1 + NAP * Exposure + (0 + NAP | Beach)
#> lme1: Richness ~ 1 + NAP + Exposure + NAP:Exposure + (1 + NAP | Beach)
#>      npar    AIC    BIC  logLik deviance   Chisq Df Pr(>Chisq)    
#> lme4    5 254.24 263.27 -122.12   244.24                          
#> lm      7 234.26 246.91 -110.13   220.26 23.9789  2  6.209e-06 ***
#> lme2    8 236.26 250.71 -110.13   220.26  0.0000  1     1.0000    
#> lme3    8 236.26 250.71 -110.13   220.26  0.0000  0               
#> lme1   10 238.20 256.27 -109.10   218.20  2.0619  2     0.3567    
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

# p小于0.05,说明全模型与简化后模型存在差异，最终采用lme1,AIC

14.8 模型诊断

sleepstudy

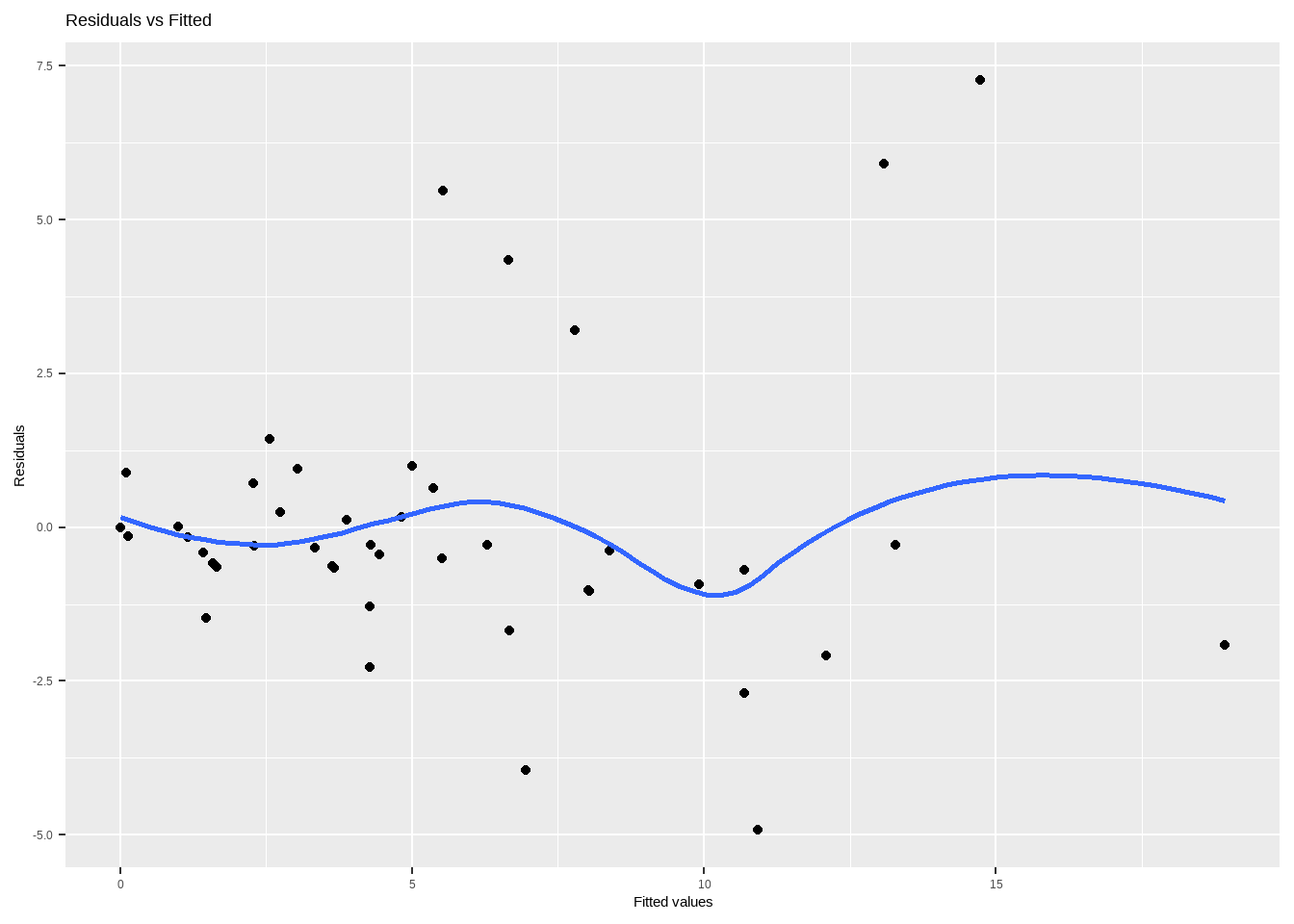
Show the code

# 拟合线性混合模型
model <- lme1
# 1. 残差图
residuals <- resid(model)
fitted <- fitted(model)
ggplot(data.frame(fitted, residuals), aes(fitted, residuals)) +
  geom_point() +
  geom_smooth(method = "loess", se = FALSE) +
  labs(title = "Residuals vs Fitted", x = "Fitted values", y = "Residuals")

Show the code


# 2. QQ图
qqnorm(residuals)
qqline(residuals)

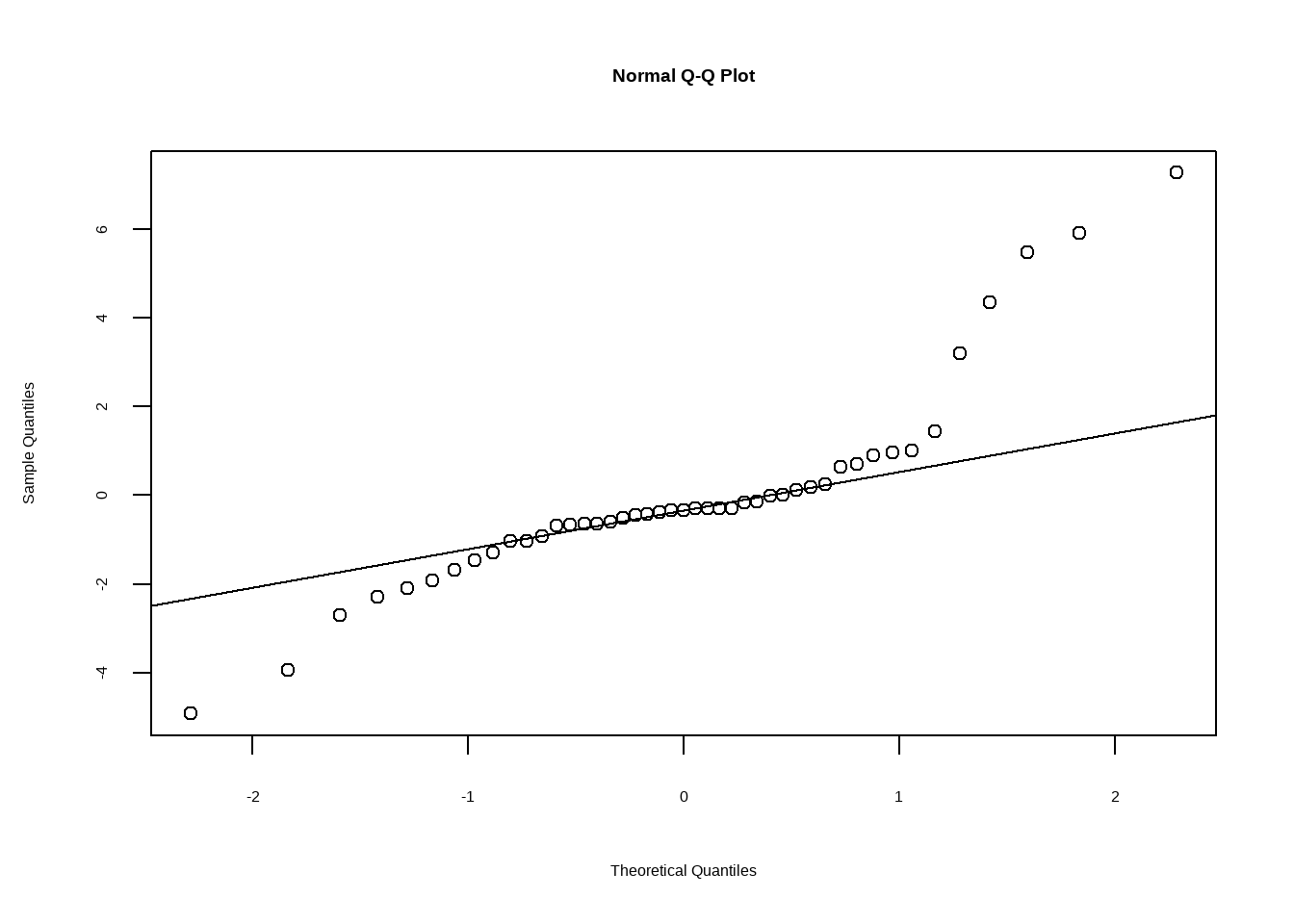
Show the code


# 3. Cook's 距离
cooksd <- cooks.distance(model)
plot(cooksd, type = "h", main = "Cook's Distance")

Show the code


# 4. 随机效应的分布
rand_dist <- ranef(model)

qqnorm(rand_dist$Beach$NAP)
qqline(rand_dist$Beach$NAP)

14.1 lme4::lmer()

14.2 随机截距+随机斜率

14.3 随机截距+固定斜率

14.4 固定截距+随机斜率

14.5 随机效应模型

14.6 线性模型：固定截距+ 固定斜率

14.7 模型选择

14.8 模型诊断

14.1 `lme4::lmer()`