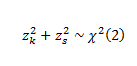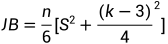统计检验与假设
Show the code
library(tidyverse)
library(ggpubr)
library(rstatix)
df <- tibble(
ctrl=c(2,6,13,5,8,9,12,11,8,10,12,14,13,6,7,4),
trt=c(8,6,8,9,12,12,14,15,16,17,14,12,11,8,10,10)
)
df
#> # A tibble: 16 × 2
#> ctrl trt
#> <dbl> <dbl>
#> 1 2 8
#> 2 6 6
#> 3 13 8
#> 4 5 9
#> 5 8 12
#> 6 9 12
#> 7 12 14
#> 8 11 15
#> 9 8 16
#> 10 10 17
#> 11 12 14
#> 12 14 12
#> 13 13 11
#> 14 6 8
#> 15 7 10
#> 16 4 10
图示法
Q-Q图
Q-Q图(或分位数-分位数图)绘制给定样本与正态分布之间的相关性。还绘制了一条 45 度参考线。在 QQ 图中,每个观测值都绘制为一个点。如果数据是正常的,则点应形成一条直线。
基于回归和相关
SAS软件规定:当样本含量n≤2000时,结果以SW检验为准,当样本含量n >2000时,结果以Kolmogorov-Smirnov(D检验)为准。
Shapiro-Wilk’s test
Shapiro-Wilk检验而是将数据的实际SD与根据数据的QQ图斜率计算的SD进行比较,并计算其比率。如果数据从高斯分布中采样,则两个值将相似,因此比率将接近1.0,而比率与1相差很大则表明为非正态分布。如果每个值均唯一,则Shapiro-Wilk检验非常有效,但如果几个值均相同,则不那么有效。推荐样本量 7~2000。
这些检验的原假设是“样本分布是正态的”。如果检验显著,则分布为非正态分布。Shapiro-Wilk 方法被广泛推荐用于正态性检验,它提供了比 K-S 更好的功率。 它基于数据与相应的正常分数之间的相关性。
正态性检验对样本量很敏感。小样本通常通过正态性检验。因此,为了做出正确的决定,将图示法和显著性检验结合起来是很重要的。如果样本数量大于 50,则首选正态 QQ 图,因为在较大的样本量下,Shapiro-Wilk 检验变得非常敏感,即使与正态的微小偏差也是如此。
Show the code
map_df(df,~ shapiro.test(.x)[c("statistic","p.value")])
#> # A tibble: 2 × 2
#> statistic p.value
#> <dbl> <dbl>
#> 1 0.961 0.676
#> 2 0.966 0.763
df %>% shapiro_test(ctrl,trt)
#> # A tibble: 2 × 3
#> variable statistic p
#> <chr> <dbl> <dbl>
#> 1 ctrl 0.961 0.676
#> 2 trt 0.966 0.763
Show the code
ToothGrowth %>%
group_by(dose) %>%
shapiro_test(len)
#> # A tibble: 3 × 4
#> dose variable statistic p
#> <dbl> <chr> <dbl> <dbl>
#> 1 0.5 len 0.941 0.247
#> 2 1 len 0.931 0.164
#> 3 2 len 0.978 0.902
Show the code
# Shapiro Wilk normality test for two variables
iris %>% shapiro_test(Sepal.Length, Petal.Width)
#> # A tibble: 2 × 3
#> variable statistic p
#> <chr> <dbl> <dbl>
#> 1 Petal.Width 0.902 0.0000000168
#> 2 Sepal.Length 0.976 0.0102
Show the code
# Multivariate normality test
mshapiro_test(iris[, 1:3])
#> # A tibble: 1 × 2
#> statistic p.value
#> <dbl> <dbl>
#> 1 0.991 0.443
基于经验分布函数(empirical distribution function)
Kolmogorov-Smirnov (K-S) test
Kolmogorov-Smirnov检验(K-S检验),这是一种非参数检验方法,用于比较一个样本的累积分布函数(CDF)与某个理论CDF的差异。需要指定总体的均值和方差
不建议使用Kolmogorov-Smirnov检验。但在大样本(>2000)实用
Show the code
ks.test(df$ctrl,"pnorm",mean=mean(df$ctrl),sd=sd(df$ctrl))
#>
#> Asymptotic one-sample Kolmogorov-Smirnov test
#>
#> data: df$ctrl
#> D = 0.13004, p-value = 0.9496
#> alternative hypothesis: two-sided
在执行单样本Kolmogorov-Smirnov检验时,数据中不应该存在“ties”,即不应该有重复的数值。如果存在重复的数值,它会影响检验的有效性,因为K-S检验对数据中的“ties”敏感。此时,可以考虑使用其他对“ties”不敏感的检验方法,例如Shapiro-Wilk检验或Lilliefors检验。
Lilliefors test
Lilliefors test 是一个修改版的K-S检验,它使用样本均值和标准差来标准化数据,然后与标准正态分布进行比较
Show the code
nortest::lillie.test(df$ctrl)
#>
#> Lilliefors (Kolmogorov-Smirnov) normality test
#>
#> data: df$ctrl
#> D = 0.13004, p-value = 0.6656
nortest::lillie.test(df$trt)
#>
#> Lilliefors (Kolmogorov-Smirnov) normality test
#>
#> data: df$trt
#> D = 0.11011, p-value = 0.87
Anderson-Darling test
Anderson-Darling test 是基于累积分布函数(CDF)的比较,通过计算观测值与理论分布之间的差异程度来评估数据的拟合程度。在R语言中,可以使用 nortest 包中的 ad.test() 函数来执行此检验。此检验的原假设同样是数据服从正态分布,如果p值小于显著性水平,则拒绝原假设,认为数据不服从正态分布。对尾部敏感,适用于中等样本量的数据
Show the code
nortest::ad.test(df$ctrl)
#>
#> Anderson-Darling normality test
#>
#> data: df$ctrl
#> A = 0.24254, p-value = 0.7247
nortest::ad.test(df$trt)
#>
#> Anderson-Darling normality test
#>
#> data: df$trt
#> A = 0.24294, p-value = 0.7233
基于卡方分布
D’Agostino-Pearson Omnibus Test
D’Agostino-Pearson test
D’Agostino-Pearson 综合检验 是基于数据的偏度和峰度来评估数据是否接近正态分布的。
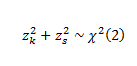
首先计算偏斜度和峰度,以量化分布在不对称性和形状方面与高斯分布的差距。然后,其计算这些值中的每一个与高斯分布的预期值之间的差异,并基于这些差异的总和,计算各P值。这是一种通用和强大的正态性检验,通常推荐使用。但值得注意的是,该建议也有例外。具体而言,当该分布的偏度和峰度非常接近正态分布的偏度和峰度,但肯定是非正态分布时,该检验将无法将该分布确定为非正态分布。
在R语言中,可以使用 moments 包中的 agostino.test() 函数来执行此检验。此检验的原假设是数据来自正态分布,如果检验的p值小于显著性水平(通常是0.05),则可以拒绝原假设,认为数据不服从正态分布。
Show the code
# 样本偏度和峰度
skewness <- moments::skewness(df$ctrl,na.rm = T)
kurtosis <- moments::kurtosis(df$ctrl,na.rm = T)
# 偏度检验
moments::agostino.test(df$ctrl)
#>
#> D'Agostino skewness test
#>
#> data: df$ctrl
#> skew = -0.20140, z = -0.41707, p-value = 0.6766
#> alternative hypothesis: data have a skewness
# 峰度检验
moments::anscombe.test(df$ctrl)
#>
#> Anscombe-Glynn kurtosis test
#>
#> data: df$ctrl
#> kurt = 1.96325, z = -0.99736, p-value = 0.3186
#> alternative hypothesis: kurtosis is not equal to 3
# D'Agostino's K² 检验
K2 <- length(df$ctrl) * (skewness^2 / 6 + (kurtosis - 3)^2 / 24)
p_value <- 1 - pchisq(K2, df = 2)
K2
#> [1] 0.8247351
p_value
#> [1] 0.6620809
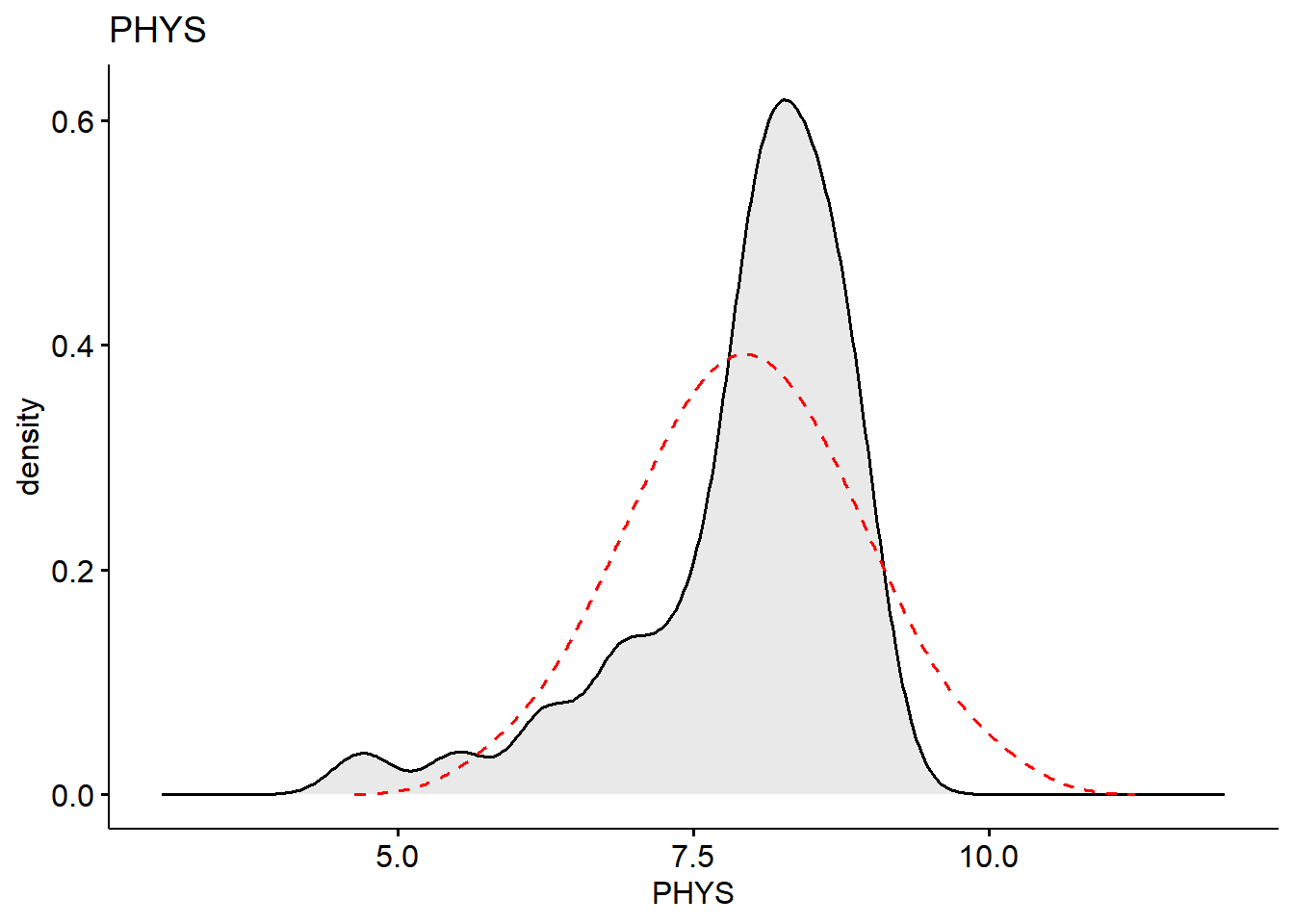
Jarque-Bera 正态性检验
Jarque-Bera检验也是一种基于样本偏度和峰度的正态性检验方法。
Show the code
if(!require(tseries)){install.packages('tseries')}
tseries::jarque.bera.test(df$ctrl)
#>
#> Jarque Bera Test
#>
#> data: df$ctrl
#> X-squared = 0.82474, df = 2, p-value = 0.6621
tseries::jarque.bera.test(df$trt)
#>
#> Jarque Bera Test
#>
#> data: df$trt
#> X-squared = 0.69681, df = 2, p-value = 0.7058
Pearson’s X2 test
Show the code
nortest::pearson.test(df$ctrl)
#>
#> Pearson chi-square normality test
#>
#> data: df$ctrl
#> P = 2.375, p-value = 0.6671
nortest::pearson.test(df$trt)
#>
#> Pearson chi-square normality test
#>
#> data: df$trt
#> P = 3.25, p-value = 0.5169
数据变换
非常偏态-倒数
1/x对于正偏态数据
1/(max(x+1) - x)对于负偏态数据
线性度和异方差性
Linearity and heteroscedasticity
Show the code
library(ggpubr)
library(moments)
data("USJudgeRatings")
df <- USJudgeRatings
head(df)
#> CONT INTG DMNR DILG CFMG DECI PREP FAMI ORAL WRIT PHYS RTEN
#> AARONSON,L.H. 5.7 7.9 7.7 7.3 7.1 7.4 7.1 7.1 7.1 7.0 8.3 7.8
#> ALEXANDER,J.M. 6.8 8.9 8.8 8.5 7.8 8.1 8.0 8.0 7.8 7.9 8.5 8.7
#> ARMENTANO,A.J. 7.2 8.1 7.8 7.8 7.5 7.6 7.5 7.5 7.3 7.4 7.9 7.8
#> BERDON,R.I. 6.8 8.8 8.5 8.8 8.3 8.5 8.7 8.7 8.4 8.5 8.8 8.7
#> BRACKEN,J.J. 7.3 6.4 4.3 6.5 6.0 6.2 5.7 5.7 5.1 5.3 5.5 4.8
#> BURNS,E.B. 6.2 8.8 8.7 8.5 7.9 8.0 8.1 8.0 8.0 8.0 8.6 8.6
Show the code
Show the code
Show the code
skewness(df$CONT, na.rm = TRUE)
#> [1] 1.085972
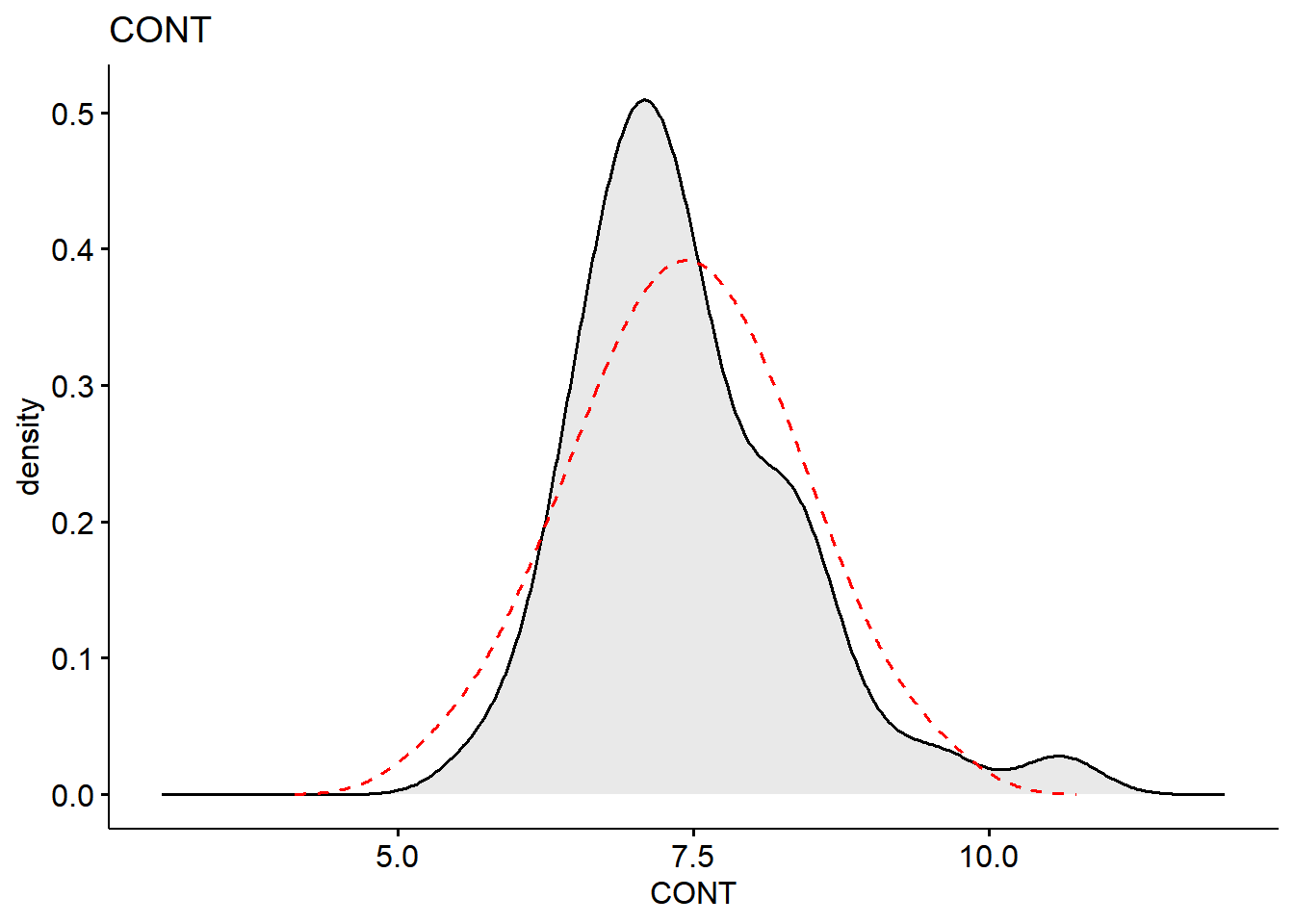
skewness(df$PHYS, na.rm = TRUE)
#> [1] -1.558215
Box-Cox 幂次变换
Show the code
bc <- car::powerTransform(df)
bc
#> Estimated transformation parameters
#> CONT INTG DMNR DILG CFMG DECI PREP
#> -0.9819079 3.8646573 3.1866054 3.0071768 3.2197291 2.8949756 2.2797376
#> FAMI ORAL WRIT PHYS RTEN
#> 2.0508085 2.4118066 2.2521739 4.9918792 3.3428550
summary(bc)
#> bcPower Transformations to Multinormality
#> Est Power Rounded Pwr Wald Lwr Bnd Wald Upr Bnd
#> CONT -0.9819 0.00 -2.7096 0.7458
#> INTG 3.8647 3.86 2.3656 5.3637
#> DMNR 3.1866 3.19 2.1669 4.2063
#> DILG 3.0072 2.00 1.9536 4.0607
#> CFMG 3.2197 3.22 2.1068 4.3326
#> DECI 2.8950 2.00 1.6568 4.1332
#> PREP 2.2797 2.00 1.5568 3.0026
#> FAMI 2.0508 2.00 1.1463 2.9553
#> ORAL 2.4118 2.00 1.8057 3.0180
#> WRIT 2.2522 2.00 1.5698 2.9346
#> PHYS 4.9919 4.99 3.1346 6.8491
#> RTEN 3.3429 3.34 2.5902 4.0955
#>
#> Likelihood ratio test that transformation parameters are equal to 0
#> (all log transformations)
#> LRT df pval
#> LR test, lambda = (0 0 0 0 0 0 0 0 0 0 0 0) 121.8881 12 < 2.22e-16
#>
#> Likelihood ratio test that no transformations are needed
#> LRT df pval
#> LR test, lambda = (1 1 1 1 1 1 1 1 1 1 1 1) 61.75316 12 1.0794e-08