14  线性混合模型

Modified

November 20, 2024

线性混合效应模型 （Linear Mixed-effect Model, LMM）用于分析具有固定效应和随机效应的数据结构。它能够处理数据中的组内相关性和个体差异，广泛应用于生态学、心理学等领域的统计分析。如果数据满足正态分布但有组内相关性，使用线性混合模型（LMM）。

Mixed Effects Models and Extensions in Ecology with R 第5章

线性混合模型的一般表达形式：

\[ Y = \mathbf{X} \beta + \mathbf{Z} \gamma + \epsilon \]

其中：

14.1 lme4::lmer()

lmer() 的表达式如下：

\[ lmer (data,formual= DV \sim Fixed\_Factor + (Random\_intercept + Random\_slope | Random\_Factor)) \]

截距中，1表示随机截距，0表示固定截距，默认截距为1。

LME 表达式 简写
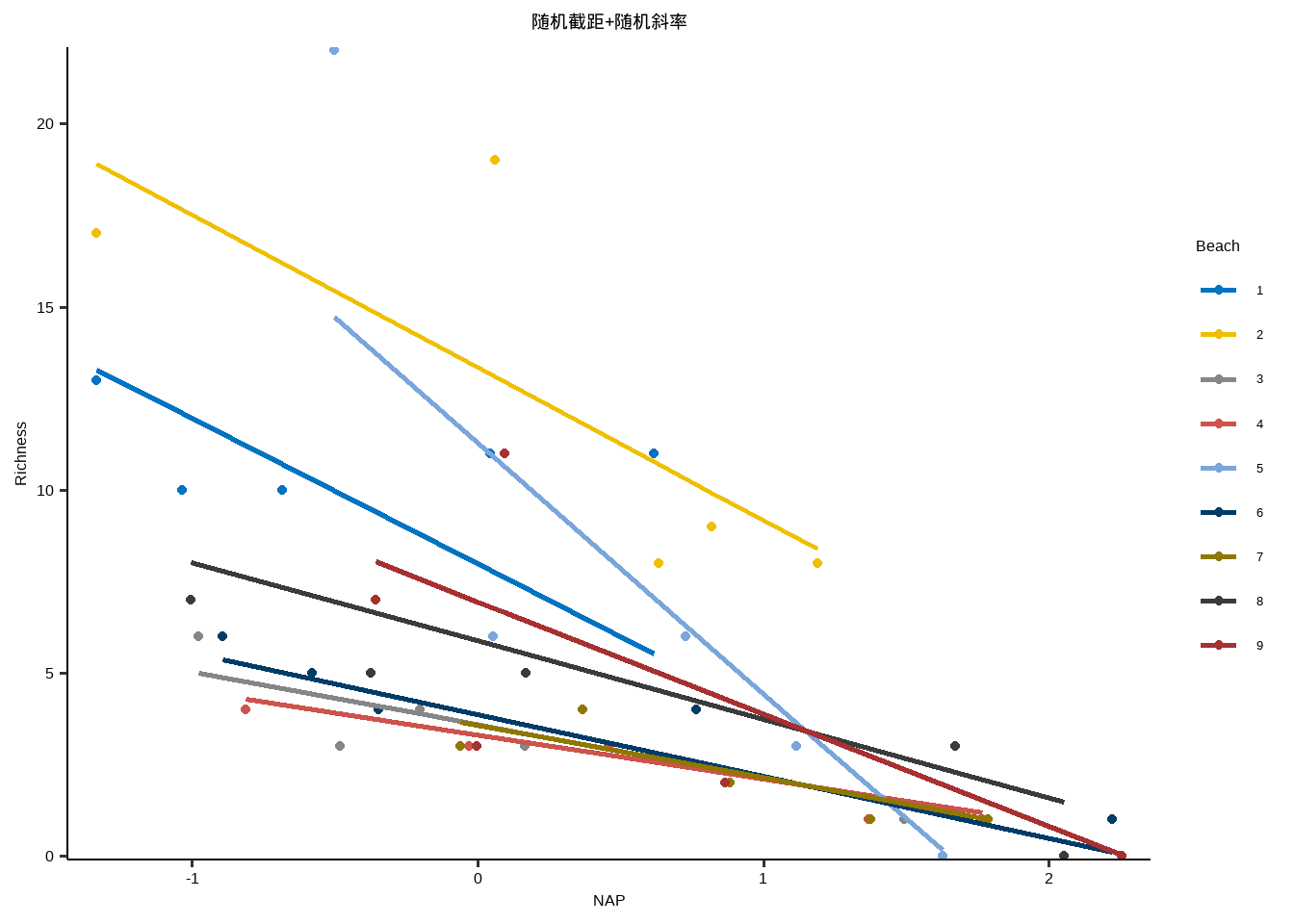
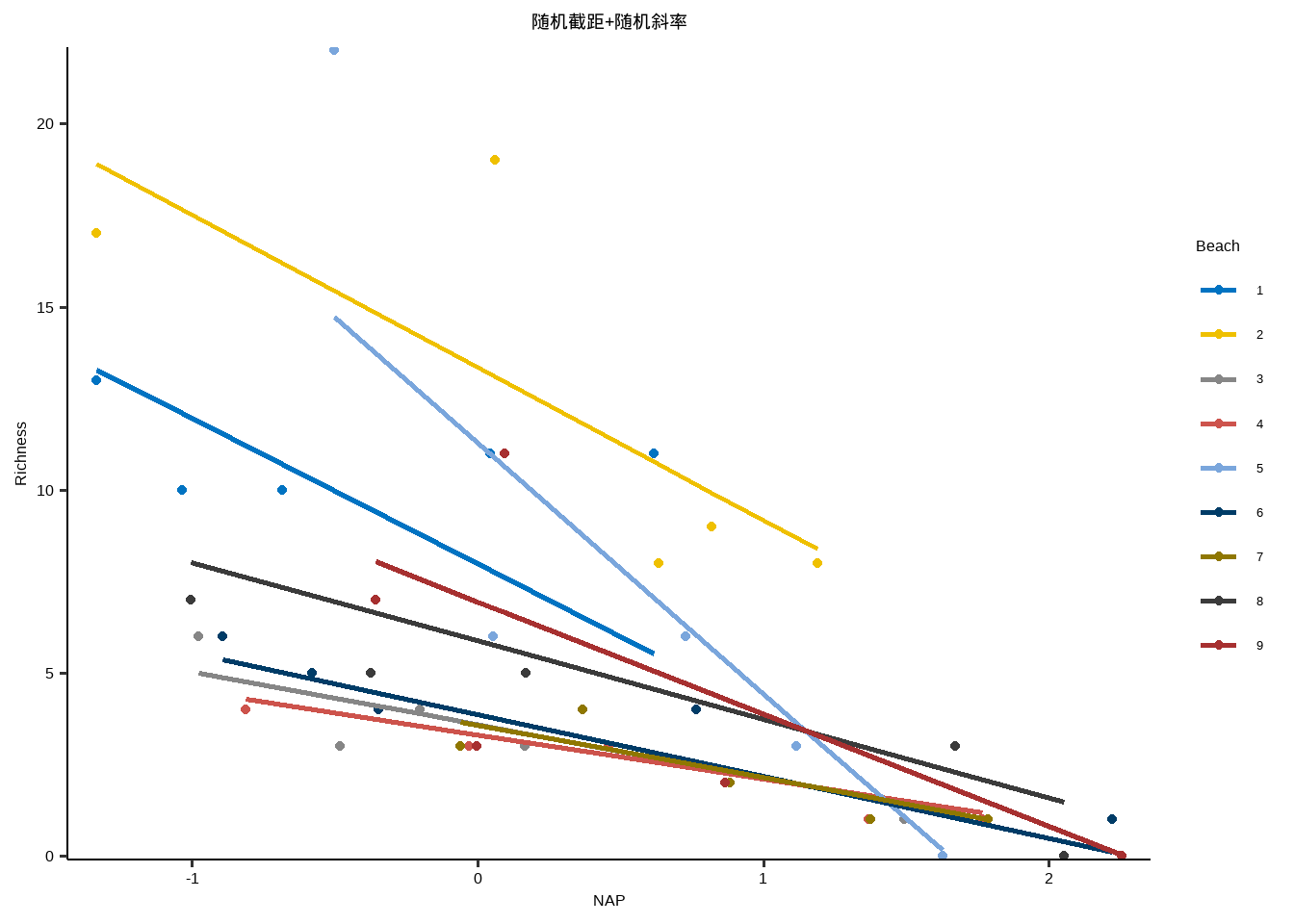
随机截距+随机斜率 y~x+( 1+x | id ) y~x+( x | id )
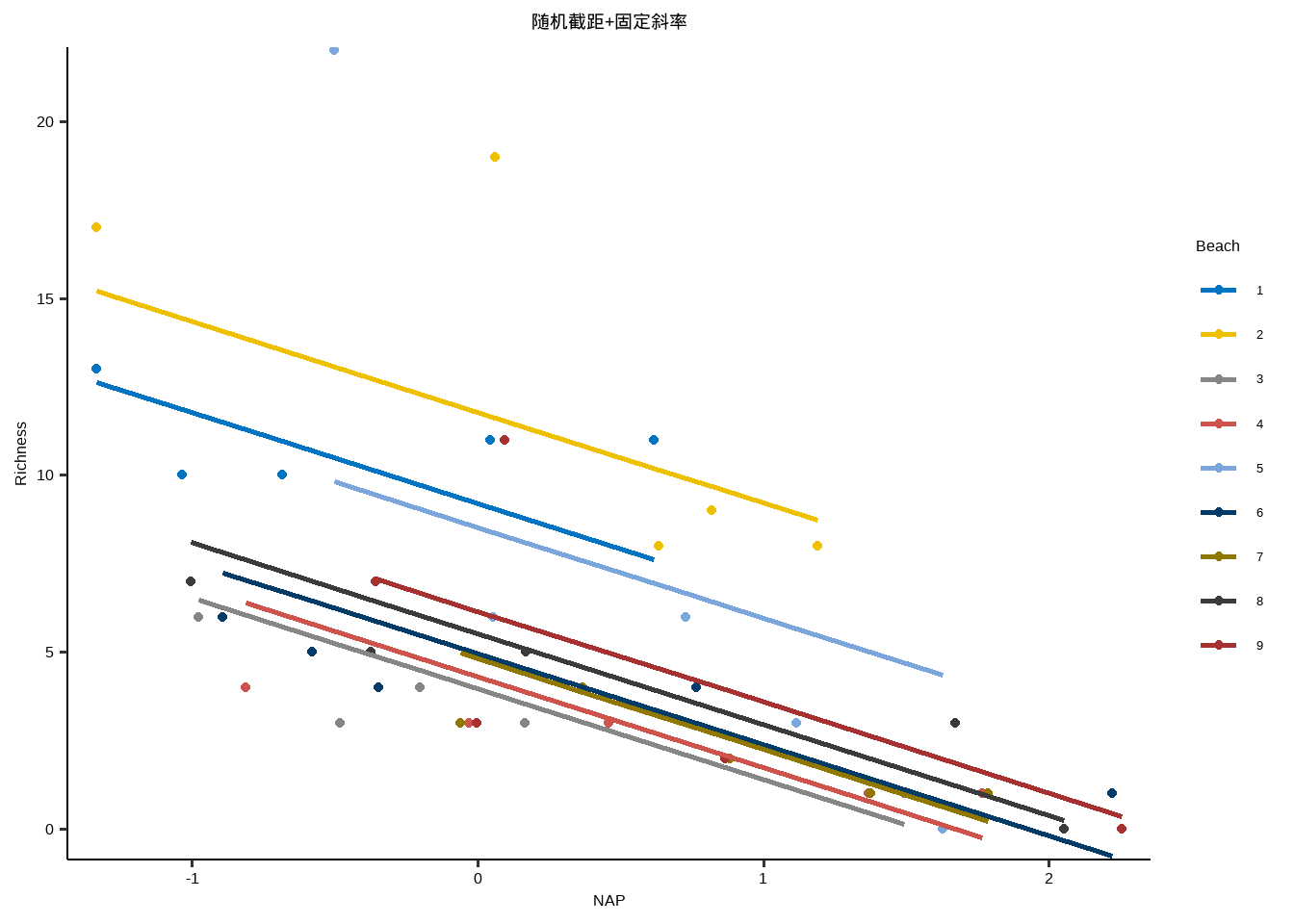
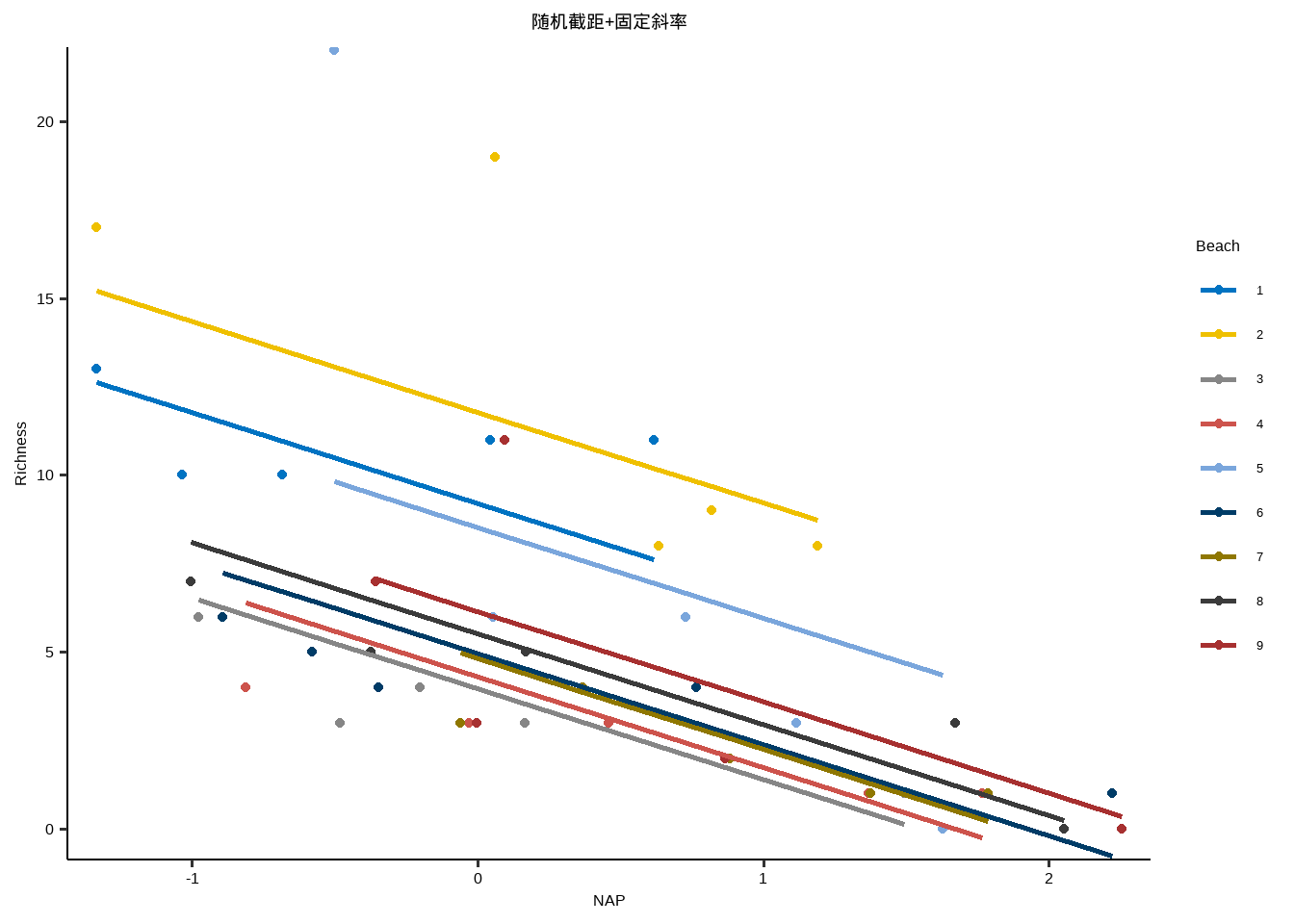
随机截距+固定斜率 y~x+( 1+1 | id ) y~x+( 1 | id )
固定截距+随机斜率 y~x+( 0+x | id ) NA
线性模型：固定截距+固定斜率 y~x NA

14.2 nlme::lme()

14.3 随机截距+随机斜率

Show the code
df_long <- read_delim("data/AED/RIKZ.txt")
df_long$Beach <- factor(df_long$Beach)
df_long$Exposure <- factor(df_long$Exposure)
head(df_long)
#> # A tibble: 6 × 5
#>   Sample Richness Exposure    NAP Beach
#>    <dbl>    <dbl> <fct>     <dbl> <fct>
#> 1      1       11 10        0.045 1    
#> 2      2       10 10       -1.04  1    
#> 3      3       13 10       -1.34  1    
#> 4      4       11 10        0.616 1    
#> 5      5       10 10       -0.684 1    
#> 6      6        8 8         1.19  2

\[ \eta_{(nrow \times 1)} = \mathbf{X}_{nrow \times 1} \beta_{1 \times 1} + \mathbf{Z}_{nrow \times 2n_{subjects}} \mathbf{\gamma}_{2n_{subjects} \times 1} + \epsilon_i \]

Z有两倍于受试者数量的列，每个受试者的随机截距和随机斜率

Show the code
library(lme4)
lme1 <- lmer(Richness ~ 1 + NAP * Exposure+ (1 + NAP |Beach) ,data = df_long)
summary(lme1)
#> Linear mixed model fit by REML ['lmerMod']
#> Formula: Richness ~ 1 + NAP * Exposure + (1 + NAP | Beach)
#>    Data: df_long
#> 
#> REML criterion at convergence: 207.2
#> 
#> Scaled residuals: 
#>      Min       1Q   Median       3Q      Max 
#> -1.92384 -0.36066 -0.13343  0.09819  2.84228 
#> 
#> Random effects:
#>  Groups   Name        Variance Std.Dev. Corr 
#>  Beach    (Intercept) 3.758    1.938         
#>           NAP         2.837    1.684    -1.00
#>  Residual             6.535    2.556         
#> Number of obs: 45, groups:  Beach, 9
#> 
#> Fixed effects:
#>                Estimate Std. Error t value
#> (Intercept)     13.3457     2.2784   5.858
#> NAP             -4.1753     2.1243  -1.965
#> Exposure10      -5.3273     2.5556  -2.085
#> Exposure11      -9.7660     2.5653  -3.807
#> NAP:Exposure10   0.1646     2.3621   0.070
#> NAP:Exposure11   2.7273     2.3715   1.150
#> 
#> Correlation of Fixed Effects:
#>             (Intr) NAP    Exps10 Exps11 NAP:E10
#> NAP         -0.770                             
#> Exposure10  -0.892  0.686                      
#> Exposure11  -0.888  0.683  0.792               
#> NAP:Expsr10  0.692 -0.899 -0.775 -0.615        
#> NAP:Expsr11  0.689 -0.896 -0.615 -0.779  0.806 
#> optimizer (nloptwrap) convergence code: 0 (OK)
#> boundary (singular) fit: see help('isSingular')
AIC(lme1)
#> [1] 227.1558
BIC(lme1)
#> [1] 245.2224
logLik(lme1)
#> 'log Lik.' -103.5779 (df=10)

2*(1-pt(-3.914605,35,lower.tail = F))
#> [1] 0.0003993968
library(broom.mixed)
tidy(lme1)
#> # A tibble: 10 × 6
#>    effect   group    term                 estimate std.error statistic
#>    <chr>    <chr>    <chr>                   <dbl>     <dbl>     <dbl>
#>  1 fixed    <NA>     (Intercept)            13.3        2.28    5.86  
#>  2 fixed    <NA>     NAP                    -4.18       2.12   -1.97  
#>  3 fixed    <NA>     Exposure10             -5.33       2.56   -2.08  
#>  4 fixed    <NA>     Exposure11             -9.77       2.57   -3.81  
#>  5 fixed    <NA>     NAP:Exposure10          0.165      2.36    0.0697
#>  6 fixed    <NA>     NAP:Exposure11          2.73       2.37    1.15  
#>  7 ran_pars Beach    sd__(Intercept)         1.94      NA      NA     
#>  8 ran_pars Beach    cor__(Intercept).NAP   -1         NA      NA     
#>  9 ran_pars Beach    sd__NAP                 1.68      NA      NA     
#> 10 ran_pars Residual sd__Observation         2.56      NA      NA

library(nlme)

nlme1 <- lme(Richness ~ 1 + NAP * Exposure,
             random = ~ 1 + NAP | Beach ,
             data = df_long,
             control = lmeControl(opt = "optim", msMaxIter = 100, msMaxEval = 5000))
summary(nlme1)
#> Linear mixed-effects model fit by REML
#>   Data: df_long 
#>        AIC      BIC    logLik
#>   227.2046 243.8402 -103.6023
#> 
#> Random effects:
#>  Formula: ~1 + NAP | Beach
#>  Structure: General positive-definite, Log-Cholesky parametrization
#>             StdDev   Corr  
#> (Intercept) 1.939709 (Intr)
#> NAP         1.689580 -0.996
#> Residual    2.554676       
#> 
#> Fixed effects:  Richness ~ 1 + NAP * Exposure 
#>                    Value Std.Error DF   t-value p-value
#> (Intercept)    13.345694  2.278989 33  5.855970  0.0000
#> NAP            -4.175271  2.128084 33 -1.961986  0.0582
#> Exposure10     -5.323695  2.556406  6 -2.082492  0.0825
#> Exposure11     -9.765613  2.566035  6 -3.805720  0.0089
#> NAP:Exposure10  0.167146  2.366467 33  0.070631  0.9441
#> NAP:Exposure11  2.726865  2.375786 33  1.147774  0.2593
#>  Correlation: 
#>                (Intr) NAP    Exps10 Exps11 NAP:E10
#> NAP            -0.767                             
#> Exposure10     -0.891  0.684                      
#> Exposure11     -0.888  0.682  0.792               
#> NAP:Exposure10  0.690 -0.899 -0.772 -0.613        
#> NAP:Exposure11  0.687 -0.896 -0.613 -0.777  0.806 
#> 
#> Standardized Within-Group Residuals:
#>        Min         Q1        Med         Q3        Max 
#> -1.9251786 -0.3608959 -0.1327685  0.0992999  2.8420571 
#> 
#> Number of Observations: 45
#> Number of Groups: 9

tidy(nlme1)
#> # A tibble: 10 × 8
#>    effect   group    term            estimate std.error    df statistic  p.value
#>    <chr>    <chr>    <chr>              <dbl>     <dbl> <dbl>     <dbl>    <dbl>
#>  1 fixed    <NA>     (Intercept)       13.3        2.28    33    5.86    1.47e-6
#>  2 fixed    <NA>     NAP               -4.18       2.13    33   -1.96    5.82e-2
#>  3 fixed    <NA>     Exposure10        -5.32       2.56     6   -2.08    8.25e-2
#>  4 fixed    <NA>     Exposure11        -9.77       2.57     6   -3.81    8.91e-3
#>  5 fixed    <NA>     NAP:Exposure10     0.167      2.37    33    0.0706  9.44e-1
#>  6 fixed    <NA>     NAP:Exposure11     2.73       2.38    33    1.15    2.59e-1
#>  7 ran_pars Beach    sd_(Intercept)     1.94      NA       NA   NA      NA      
#>  8 ran_pars Beach    cor_NAP.(Inter…   -0.996     NA       NA   NA      NA      
#>  9 ran_pars Beach    sd_NAP             1.69      NA       NA   NA      NA      
#> 10 ran_pars Residual sd_Observation     2.55      NA       NA   NA      NA

这个模型的公式可以分解为：

  • 固定效应部分：Richness 的预测由截距、NAP（数值变量）和 Exposure（分类变量，包含 Exposure10 和 Exposure11）及其交互项构成。

  • 随机效应部分：Beach 作为随机因子，包含随机截距和随机斜率（NAP）。

Show the code
# 标准化模型残差分布
quantile(residuals(lme1,type="pearson",scaled=T))
#>         0%        25%        50%        75%       100% 
#> -1.9238372 -0.3606612 -0.1334336  0.0981939  2.8422803

# 随机因子随机效应和显著性检验
ranef(lme1)
#> $Beach
#>     (Intercept)           NAP
#> 1 -4.274356e-02  3.713708e-02
#> 2 -2.709479e-14  2.354089e-14
#> 3  3.819348e-03 -3.318381e-03
#> 4 -2.741786e-01  2.382158e-01
#> 5  3.269522e+00 -2.840673e+00
#> 6  2.736093e-01 -2.377212e-01
#> 7 -3.250033e-03  2.823741e-03
#> 8 -2.148947e+00  1.867079e+00
#> 9 -1.077831e+00  9.364564e-01
#> 
#> with conditional variances for "Beach"
lmerTest::ranova(lme1)
#> ANOVA-like table for random-effects: Single term deletions
#> 
#> Model:
#> Richness ~ NAP + Exposure + (1 + NAP | Beach) + NAP:Exposure
#>                          npar  logLik    AIC    LRT Df Pr(>Chisq)
#> <none>                     10 -103.58 227.16                     
#> NAP in (1 + NAP | Beach)    8 -105.67 227.35 4.1935  2     0.1229

# 查看固定效应和显著性检验
coef(lme1)
#> $Beach
#>   (Intercept)       NAP Exposure10 Exposure11 NAP:Exposure10 NAP:Exposure11
#> 1    13.30295 -4.138134  -5.327265  -9.766048      0.1646123       2.727307
#> 2    13.34569 -4.175271  -5.327265  -9.766048      0.1646123       2.727307
#> 3    13.34951 -4.178590  -5.327265  -9.766048      0.1646123       2.727307
#> 4    13.07152 -3.937055  -5.327265  -9.766048      0.1646123       2.727307
#> 5    16.61522 -7.015944  -5.327265  -9.766048      0.1646123       2.727307
#> 6    13.61930 -4.412992  -5.327265  -9.766048      0.1646123       2.727307
#> 7    13.34244 -4.172447  -5.327265  -9.766048      0.1646123       2.727307
#> 8    11.19675 -2.308192  -5.327265  -9.766048      0.1646123       2.727307
#> 9    12.26786 -3.238815  -5.327265  -9.766048      0.1646123       2.727307
#> 
#> attr(,"class")
#> [1] "coef.mer"
anova(lme1)
#> Analysis of Variance Table
#>              npar  Sum Sq Mean Sq F value
#> NAP             1 124.279 124.279 19.0178
#> Exposure        2 142.983  71.492 10.9400
#> NAP:Exposure    2  22.308  11.154  1.7068

#  查看 类和方法
class(lme1)
#> [1] "lmerMod"
#> attr(,"package")
#> [1] "lme4"
# methods(class = "lmerMod")

# confint(lme1,level = 0.95)

14.4 随机截距+固定斜率

\[ \eta_{(nrow \ \times 1)}=\mathbf{X_{nrow×1}}\beta_{1\times1} +Z_{nrow\times n_{subjects}} \mathbf{\gamma}_{n_{subjects}\times 1}+\epsilon_i \]

Z有一倍于受试者数量的列，每个受试者的随机截距。

Show the code
lme2 <- lmer(Richness ~ 1 + NAP+ (1 |Beach) ,data = df_long)
summary(lme2)
#> Linear mixed model fit by REML ['lmerMod']
#> Formula: Richness ~ 1 + NAP + (1 | Beach)
#>    Data: df_long
#> 
#> REML criterion at convergence: 239.5
#> 
#> Scaled residuals: 
#>     Min      1Q  Median      3Q     Max 
#> -1.4227 -0.4848 -0.1576  0.2519  3.9794 
#> 
#> Random effects:
#>  Groups   Name        Variance Std.Dev.
#>  Beach    (Intercept) 8.668    2.944   
#>  Residual             9.362    3.060   
#> Number of obs: 45, groups:  Beach, 9
#> 
#> Fixed effects:
#>             Estimate Std. Error t value
#> (Intercept)   6.5819     1.0958   6.007
#> NAP          -2.5684     0.4947  -5.192
#> 
#> Correlation of Fixed Effects:
#>     (Intr)
#> NAP -0.157
AIC(lme2)
#> [1] 247.4802
BIC(lme2)
#> [1] 254.7069
logLik(lme2)
#> 'log Lik.' -119.7401 (df=4)

2*(1-pt(6.007,35,lower.tail = T))
#> [1] 7.558855e-07



nlme2 <- lme(Richness ~ 1 + NAP * Exposure,random= ~ 1 |Beach ,data = df_long)
summary(nlme2)
#> Linear mixed-effects model fit by REML
#>   Data: df_long 
#>        AIC      BIC    logLik
#>   227.3493 240.6578 -105.6747
#> 
#> Random effects:
#>  Formula: ~1 | Beach
#>         (Intercept) Residual
#> StdDev:   0.5138683 2.971793
#> 
#> Fixed effects:  Richness ~ 1 + NAP * Exposure 
#>                    Value Std.Error DF   t-value p-value
#> (Intercept)    13.345694  1.483557 33  8.995739  0.0000
#> NAP            -4.175271  1.505110 33 -2.774063  0.0090
#> Exposure10     -5.544983  1.657659  6 -3.345069  0.0155
#> Exposure11     -9.730595  1.670518  6 -5.824898  0.0011
#> NAP:Exposure10  0.671731  1.643864 33  0.408629  0.6855
#> NAP:Exposure11  2.688806  1.656743 33  1.622947  0.1141
#>  Correlation: 
#>                (Intr) NAP    Exps10 Exps11 NAP:E10
#> NAP            -0.278                             
#> Exposure10     -0.895  0.249                      
#> Exposure11     -0.888  0.247  0.795               
#> NAP:Exposure10  0.255 -0.916 -0.276 -0.226        
#> NAP:Exposure11  0.253 -0.908 -0.226 -0.296  0.832 
#> 
#> Standardized Within-Group Residuals:
#>        Min         Q1        Med         Q3        Max 
#> -1.5652904 -0.4386841 -0.1164805  0.1783113  4.1098230 
#> 
#> Number of Observations: 45
#> Number of Groups: 9

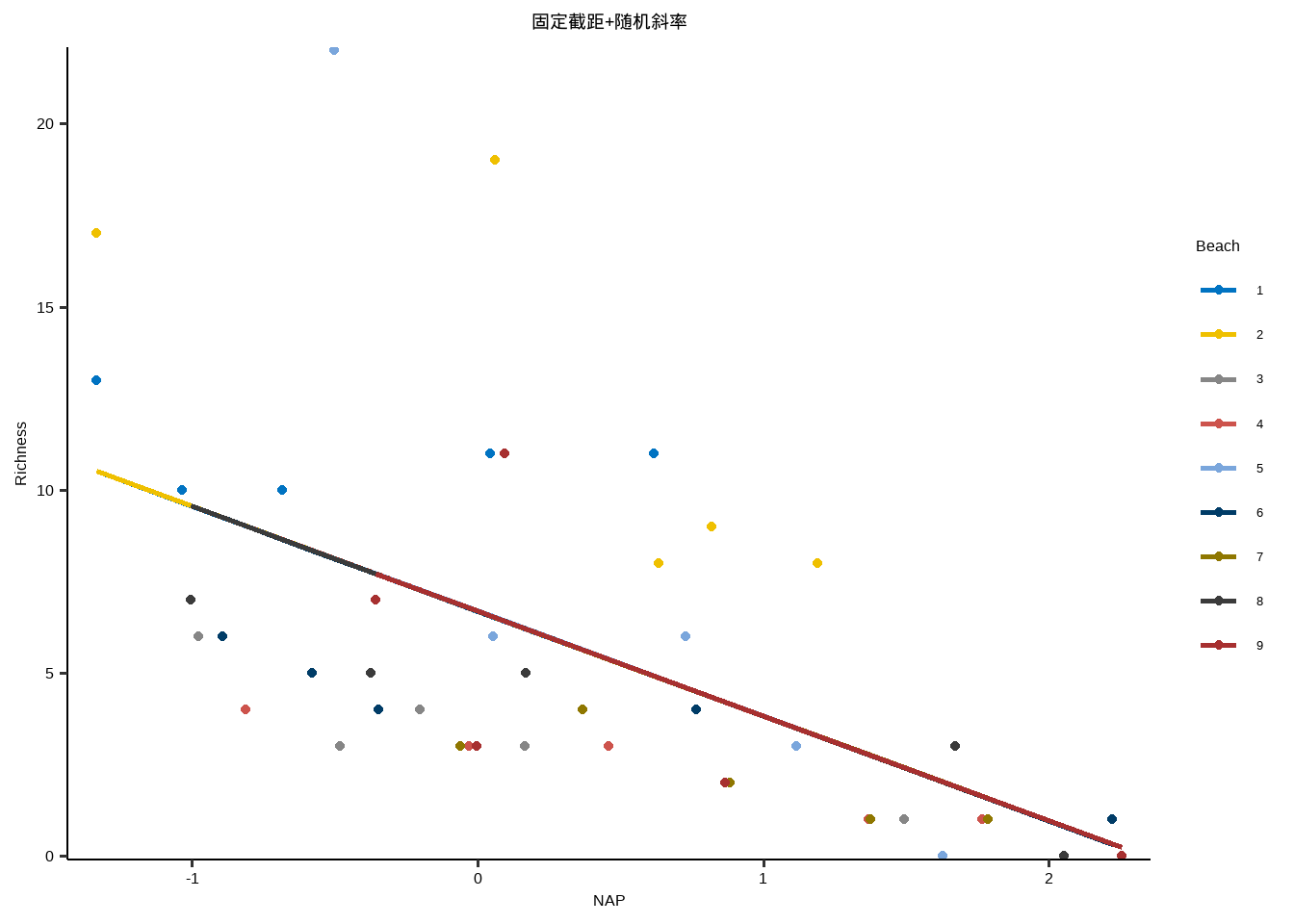
14.5 固定截距+随机斜率

\[ \eta_{(nrow \times 1)} = \mathbf{X}_{nrow \times 1} \beta_{1 \times 1} + \mathbf{Z}_{nrow \times n_{subjects}} \mathbf{\gamma}_{n_{subjects} \times 1} + \epsilon_i \]

Z 有一倍于受试者数量的列，每个受试者的随机斜率。

Show the code
lme3 <- lmer(Richness ~ 1 +  NAP+ (0 + NAP |Beach) ,data = df_long)
summary(lme3)
#> Linear mixed model fit by REML ['lmerMod']
#> Formula: Richness ~ 1 + NAP + (0 + NAP | Beach)
#>    Data: df_long
#> 
#> REML criterion at convergence: 252.2
#> 
#> Scaled residuals: 
#>     Min      1Q  Median      3Q     Max 
#> -1.2182 -0.6636 -0.1930  0.3253  3.3347 
#> 
#> Random effects:
#>  Groups   Name Variance Std.Dev.
#>  Beach    NAP   0.00    0.00    
#>  Residual      17.31    4.16    
#> Number of obs: 45, groups:  Beach, 9
#> 
#> Fixed effects:
#>             Estimate Std. Error t value
#> (Intercept)   6.6857     0.6578  10.164
#> NAP          -2.8669     0.6307  -4.545
#> 
#> Correlation of Fixed Effects:
#>     (Intr)
#> NAP -0.333
#> optimizer (nloptwrap) convergence code: 0 (OK)
#> boundary (singular) fit: see help('isSingular')

nlme3 <- lme(Richness ~ 1 + NAP,random= ~ 0+NAP |Beach ,data = df_long)
summary(nlme3)
#> Linear mixed-effects model fit by REML
#>   Data: df_long 
#>       AIC      BIC    logLik
#>   260.201 267.2458 -126.1005
#> 
#> Random effects:
#>  Formula: ~0 + NAP | Beach
#>                  NAP Residual
#> StdDev: 0.0001127408 4.159929
#> 
#> Fixed effects:  Richness ~ 1 + NAP 
#>                 Value Std.Error DF   t-value p-value
#> (Intercept)  6.685662 0.6577579 35 10.164320   0e+00
#> NAP         -2.866853 0.6307186 35 -4.545376   1e-04
#>  Correlation: 
#>     (Intr)
#> NAP -0.333
#> 
#> Standardized Within-Group Residuals:
#>        Min         Q1        Med         Q3        Max 
#> -1.2181663 -0.6636488 -0.1930031  0.3253447  3.3347473 
#> 
#> Number of Observations: 45
#> Number of Groups: 9

14.6 随机效应模型

Show the code

lme4 <- lmer(Richness ~ 1 + (1|Beach) ,data = df_long)
summary(lme4)
#> Linear mixed model fit by REML ['lmerMod']
#> Formula: Richness ~ 1 + (1 | Beach)
#>    Data: df_long
#> 
#> REML criterion at convergence: 261.1
#> 
#> Scaled residuals: 
#>     Min      1Q  Median      3Q     Max 
#> -1.7797 -0.5070 -0.0980  0.2547  3.8063 
#> 
#> Random effects:
#>  Groups   Name        Variance Std.Dev.
#>  Beach    (Intercept) 10.48    3.237   
#>  Residual             15.51    3.938   
#> Number of obs: 45, groups:  Beach, 9
#> 
#> Fixed effects:
#>             Estimate Std. Error t value
#> (Intercept)    5.689      1.228   4.631

nlme4 <- lme(Richness ~ 1 ,random= ~ 1 |Beach ,data = df_long)
summary(nlme4)
#> Linear mixed-effects model fit by REML
#>   Data: df_long 
#>        AIC      BIC    logLik
#>   267.1142 272.4668 -130.5571
#> 
#> Random effects:
#>  Formula: ~1 | Beach
#>         (Intercept) Residual
#> StdDev:    3.237112 3.938415
#> 
#> Fixed effects:  Richness ~ 1 
#>                Value Std.Error DF  t-value p-value
#> (Intercept) 5.688889  1.228419 36 4.631066       0
#> 
#> Standardized Within-Group Residuals:
#>         Min          Q1         Med          Q3         Max 
#> -1.77968689 -0.50704111 -0.09795286  0.25468670  3.80631705 
#> 
#> Number of Observations: 45
#> Number of Groups: 9

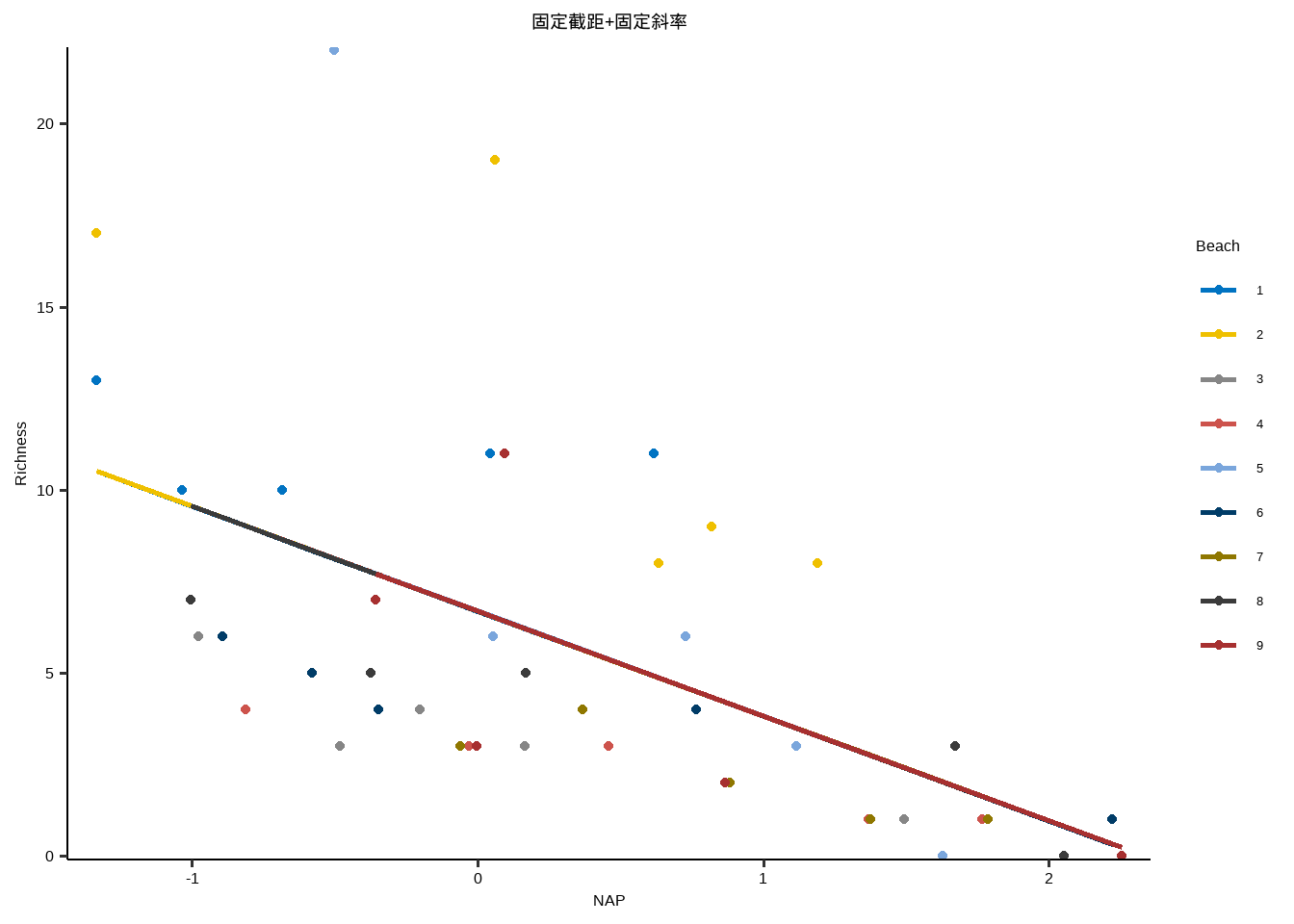
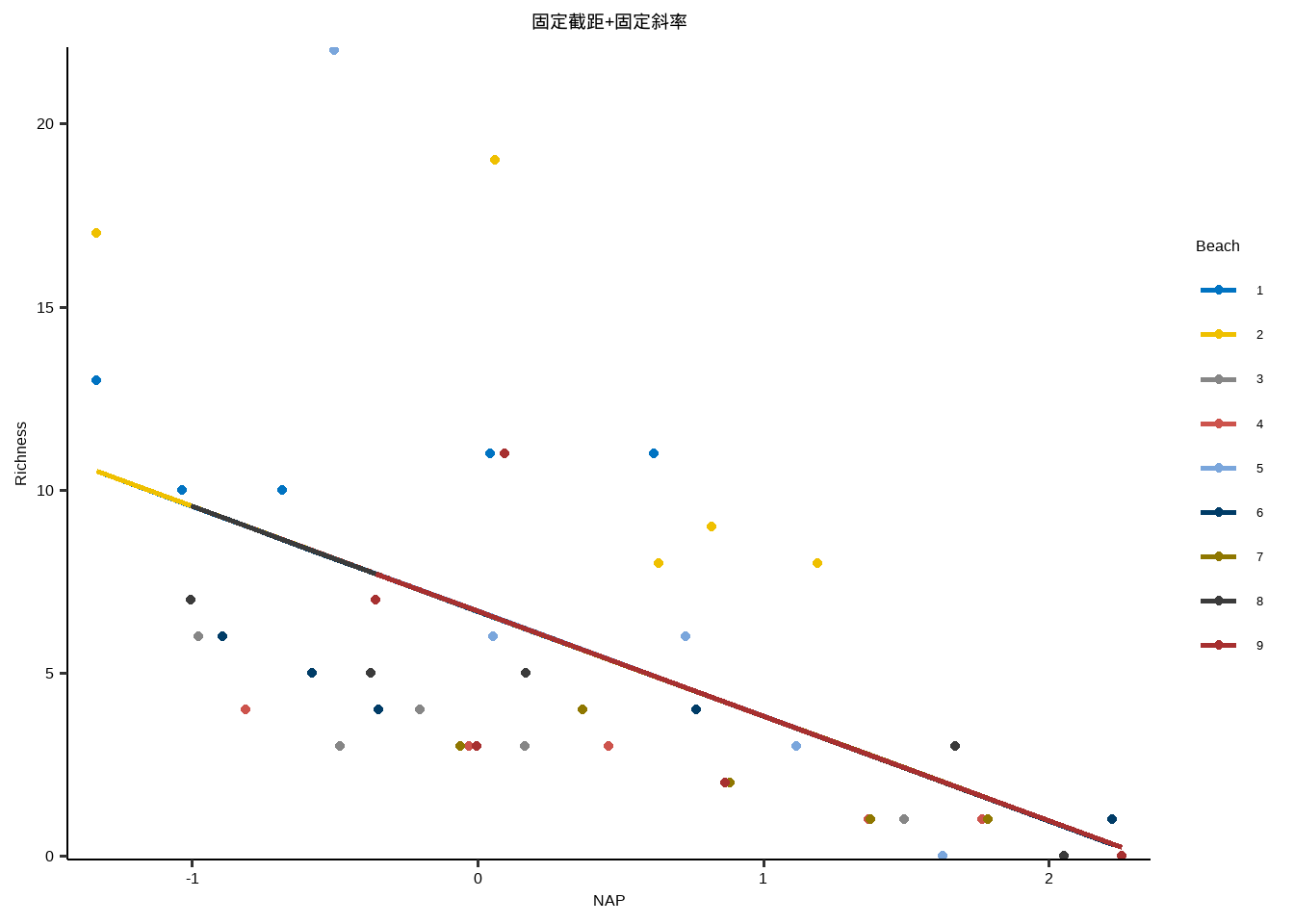
14.7 线性模型：固定截距+ 固定斜率

Show the code
lm <- lm(Richness ~ 1 + NAP ,data = df_long)
lm
#> 
#> Call:
#> lm(formula = Richness ~ 1 + NAP, data = df_long)
#> 
#> Coefficients:
#> (Intercept)          NAP  
#>       6.686       -2.867

14.8 模型选择

限制最大似然法REML

  1. 赤池信息准则（AIC）

    \[ kIC=−2log(\mathcal{L})+2k\]

    其中：

    • \(\mathcal{L}\) 是似然函数。

    • \(k\) 是模型参数的数量。

  2. 贝叶斯信息准则（BIC）

    \[ BIC=−2log(\mathcal{L})+klog(n) \]

    其中：

    • \(n\) 是样本量。
Show the code

plot_lme <- function(model, title) {
    ggplot(df_long, aes(NAP, Richness, group = Beach, color = Beach)) +
        geom_point() +
        geom_line(
            data =  bind_cols(df_long, .pred = predict(model, df_long)),
            mapping = aes(y = .pred),
            linewidth = 1
        ) +
        labs(title = title)+
        scale_x_continuous(expand = (mult=c(0,.1)))+
        scale_y_continuous(expand = (mult=c(0,.1)))+
    ggsci::scale_color_jco() +
        ggpubr::theme_pubr() +
        theme(legend.position = "right",
              plot.title = element_text(hjust = .5))
}


lme_plot <- map2(list(lme1,lme2,lme3,lm),list("随机截距+随机斜率","随机截距+固定斜率","固定截距+随机斜率","固定截距+固定斜率"),plot_lme)


lme_plot
#> [[1]]

#> 
#> [[2]]

#> 
#> [[3]]

#> 
#> [[4]]

Show the code
anova(lme1,lme2,lme3)
#> Data: df_long
#> Models:
#> lme2: Richness ~ 1 + NAP + (1 | Beach)
#> lme3: Richness ~ 1 + NAP + (0 + NAP | Beach)
#> lme1: Richness ~ 1 + NAP * Exposure + (1 + NAP | Beach)
#>      npar    AIC    BIC  logLik deviance  Chisq Df Pr(>Chisq)    
#> lme2    4 249.83 257.06 -120.92   241.83                         
#> lme3    4 261.95 269.18 -126.98   253.95  0.000  0               
#> lme1   10 238.20 256.27 -109.10   218.20 35.754  6  3.077e-06 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
anova(lme1,lme2,lme3,lme4,lm)
#> Data: df_long
#> Models:
#> lme4: Richness ~ 1 + (1 | Beach)
#> lm: Richness ~ 1 + NAP
#> lme2: Richness ~ 1 + NAP + (1 | Beach)
#> lme3: Richness ~ 1 + NAP + (0 + NAP | Beach)
#> lme1: Richness ~ 1 + NAP * Exposure + (1 + NAP | Beach)
#>      npar    AIC    BIC  logLik deviance  Chisq Df Pr(>Chisq)    
#> lme4    3 269.30 274.72 -131.65   263.30                         
#> lm      3 259.95 265.37 -126.98   253.95  9.350  0               
#> lme2    4 249.83 257.06 -120.92   241.83 12.124  1  0.0004977 ***
#> lme3    4 261.95 269.18 -126.98   253.95  0.000  0               
#> lme1   10 238.20 256.27 -109.10   218.20 35.754  6  3.077e-06 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

# p小于0.05,说明全模型与简化后模型存在差异，最终采用lme1,AIC

14.9 模型诊断

sleepstudy

Show the code
# 拟合线性混合模型
model <- lme1
# 1. 残差图
residuals <- resid(model)
fitted <- fitted(model)
ggplot(data.frame(fitted, residuals), aes(fitted, residuals)) +
  geom_point() +
  geom_smooth(method = "loess", se = FALSE) +
  labs(title = "Residuals vs Fitted", x = "Fitted values", y = "Residuals")

Show the code

# 2. QQ图
qqnorm(residuals)
qqline(residuals)

Show the code

# 3. Cook's 距离
cooksd <- cooks.distance(model)
plot(cooksd, type = "h", main = "Cook's Distance")

Show the code

# 4. 随机效应的分布
rand_dist <- ranef(model)

qqnorm(rand_dist$Beach$NAP)
qqline(rand_dist$Beach$NAP)