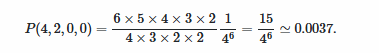描述性统计学

基本概念

• 同质 (Homogeneity)：指数据样本的同质性，即样本中各个个体之间的相似性或一致性。

• 变异 (Variation)：指数据样本中各个个体之间的差异性或变化程度。

• 总体 (Population)：研究对象的全部个体的集合。描述总体特征的统计学指标称为参数 (Parameter)。

• 样本 (Sample)：从总体中抽取的一部分个体。由样本计算出的特征指标称为统计量 (Statistic)。

• 变量 (Variable)：随机变量的简称，是研究对象的属性或特征，可以在不同个体之间或同一个体在不同时间上取不同值。

• 数据 (Data)：变量的观测值

数据类型及其分布

定量数据（quantitative data）

连续型

1. 正态分布：t 检验，方差分析，相关性检验

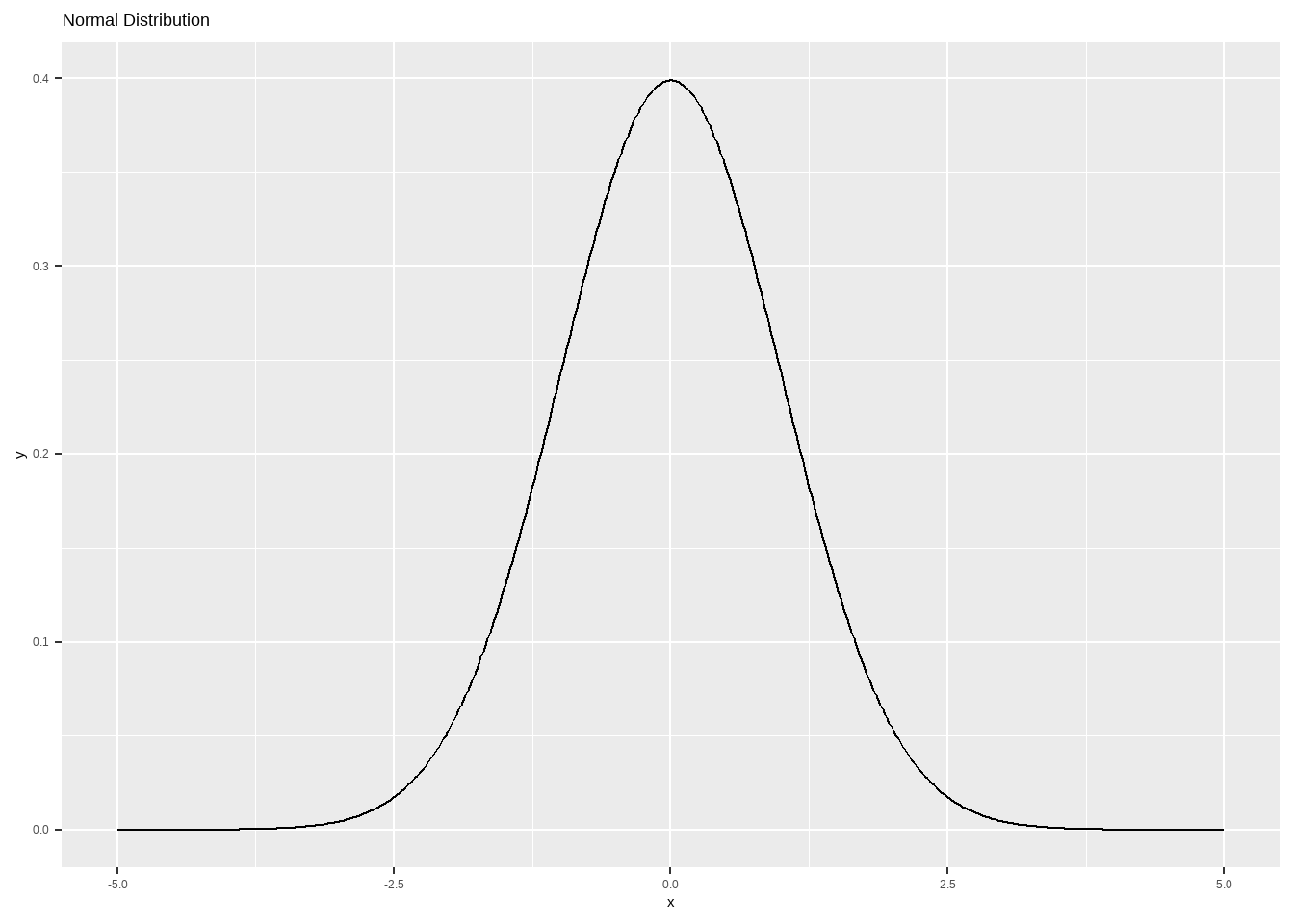
\[ f(x)= \frac{1}{\sqrt{2πσ^2}} e^{\frac {−(x−μ) ^2 }{2σ^2 }} \]

其中，\(\mu\)是均值， \(\sigma\)是标准差

library(ggplot2)
library(tibble)
# 标准正态分布
normal_data <- tibble(x = seq(-5, 5, length.out = 1000),
                      y = dnorm(x, mean = 0, sd = 1))


ggplot(normal_data, aes(x = x, y = y)) +
    geom_line() +
    ggtitle("Normal Distribution")

2. 对数正态分布：非参数检验

3. 指数分布：广义线性模型，对数秩（log-rank ）检验

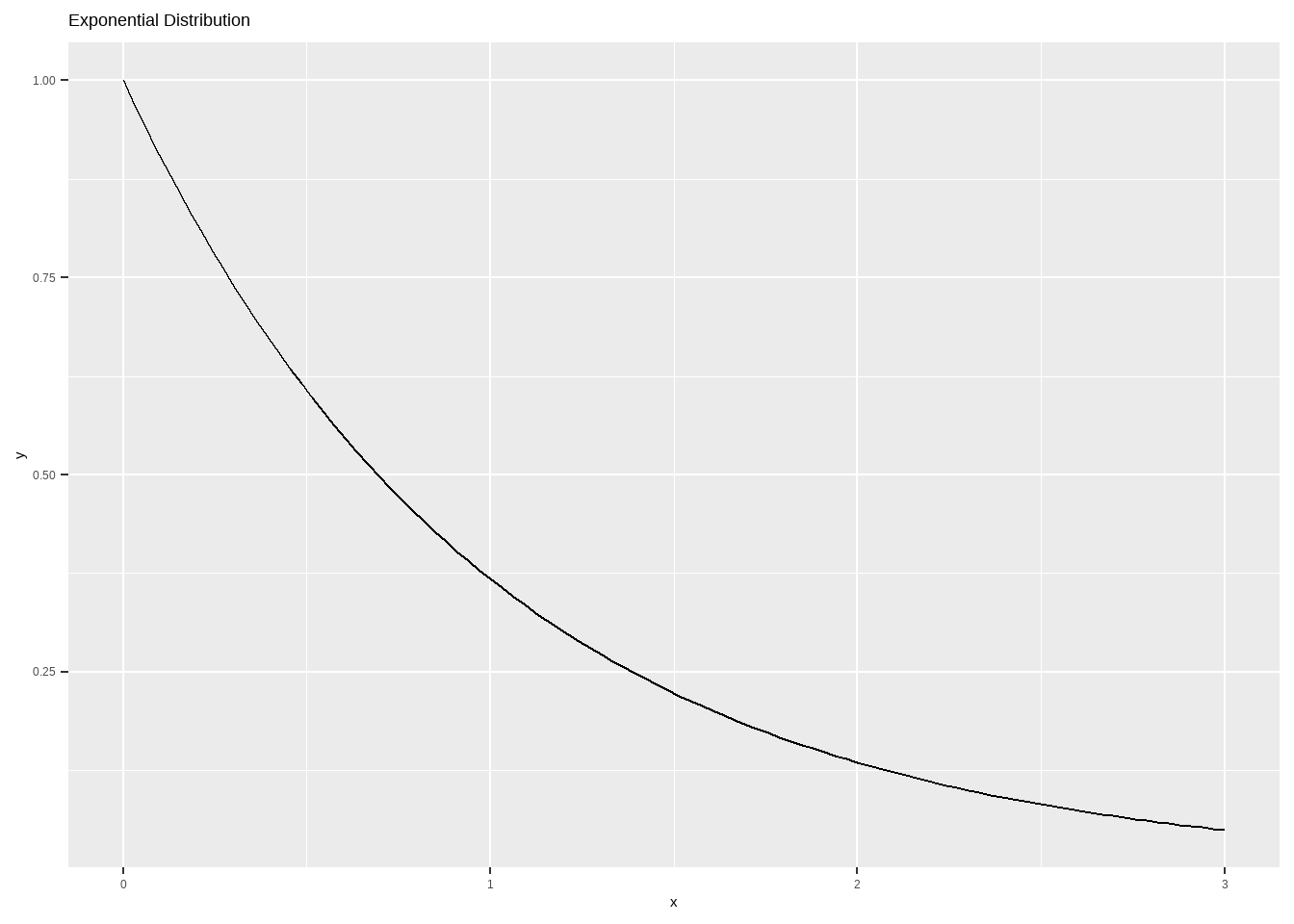
\[ f(x)=λe^{−λx}，x\ge 0 \]

其中，默认(rate)：\(\lambda = 1\)。

# 指数分布
exponential_data <- tibble(x = seq(0, 3, length.out = 100),
                           y = dexp(x, rate = 1))


ggplot(exponential_data, aes(x = x, y = y)) +
    geom_line() +
    ggtitle("Exponential Distribution")

4. 均匀分布

离散型

1. 二项分布

伯努利分布

Bernoulli 试验

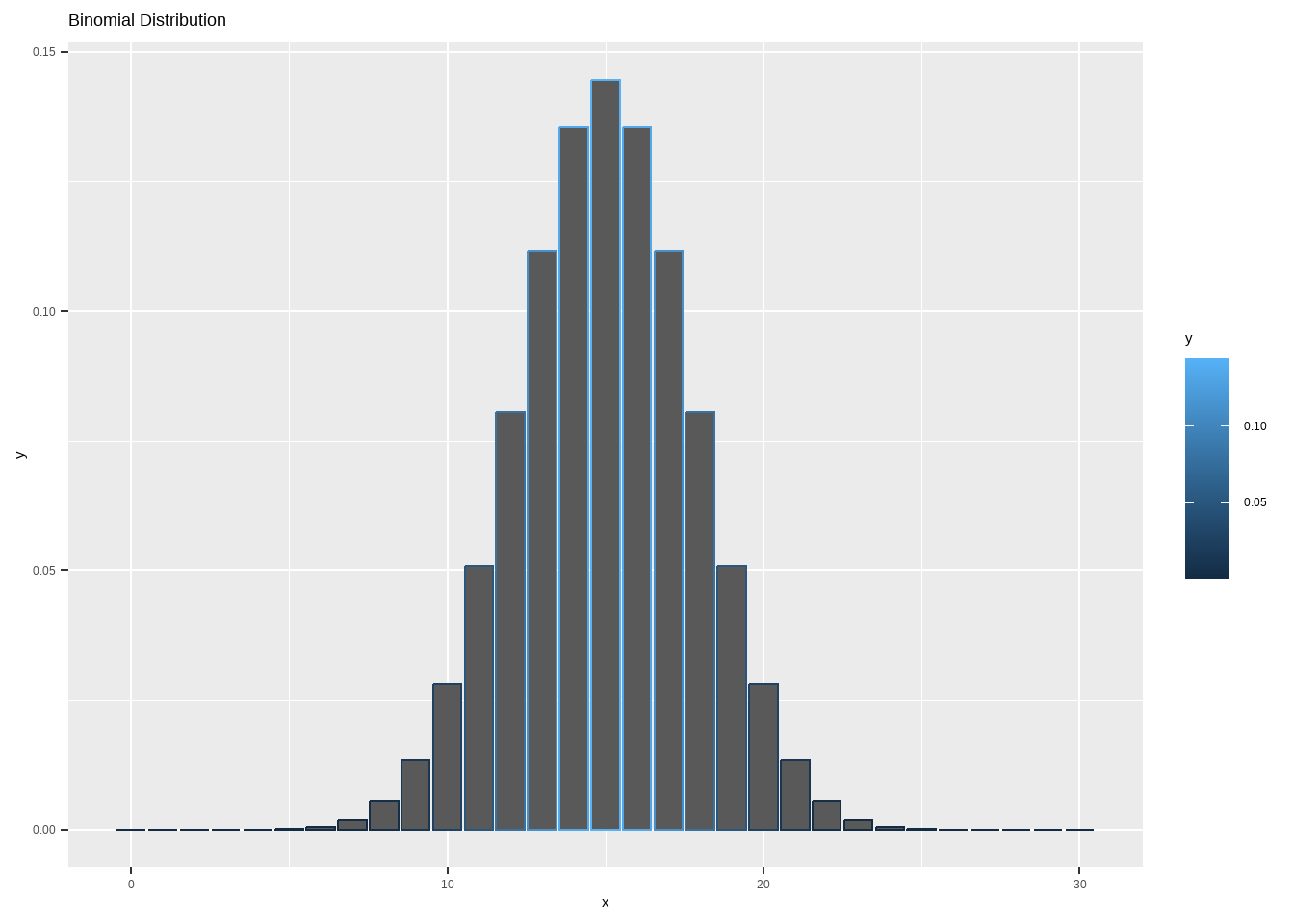
\[ P(x)=\binom{n}{x}p^x(1-p)^{n-x} \]

# 二项分布
binomial_data <- tibble(x = 0:30, y = dbinom(x, size = 30, prob = 0.5))

ggplot(binomial_data, aes(x = x, y = y, color = y)) +
    geom_col() +
    ggtitle("Binomial Distribution")

2. 负二项分布：DESeq2 差异分析

\[ P(x)=\frac{\Gamma(x+n)}{\Gamma(n)\ x!}p^n(1-p)^x \]

其中，均值 \(\mu = \frac{n(1-p)}{p}\)，方差 \(\frac{(1-p)}{p^2}\)。

# 负二项分布
negative_binomial_data <- tibble(x = 0:20, y =  dnbinom(x, size = 1, prob = 0.5))

ggplot(negative_binomial_data, aes(x = x, y = y)) +
    geom_bar(stat = "identity") +
    ggtitle("Negative Binomial Distribution")

3. 泊松分布

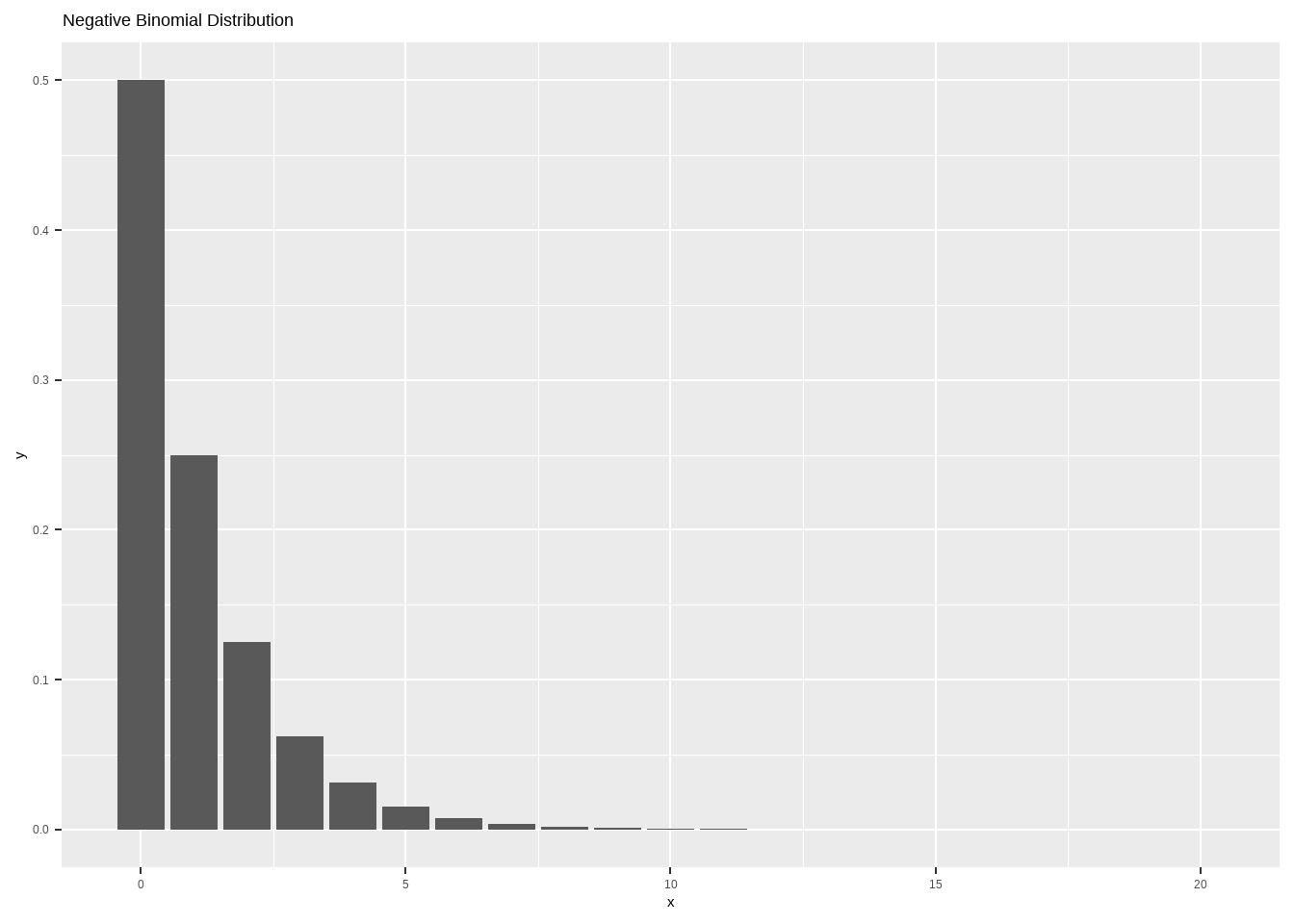
DNA 点突变

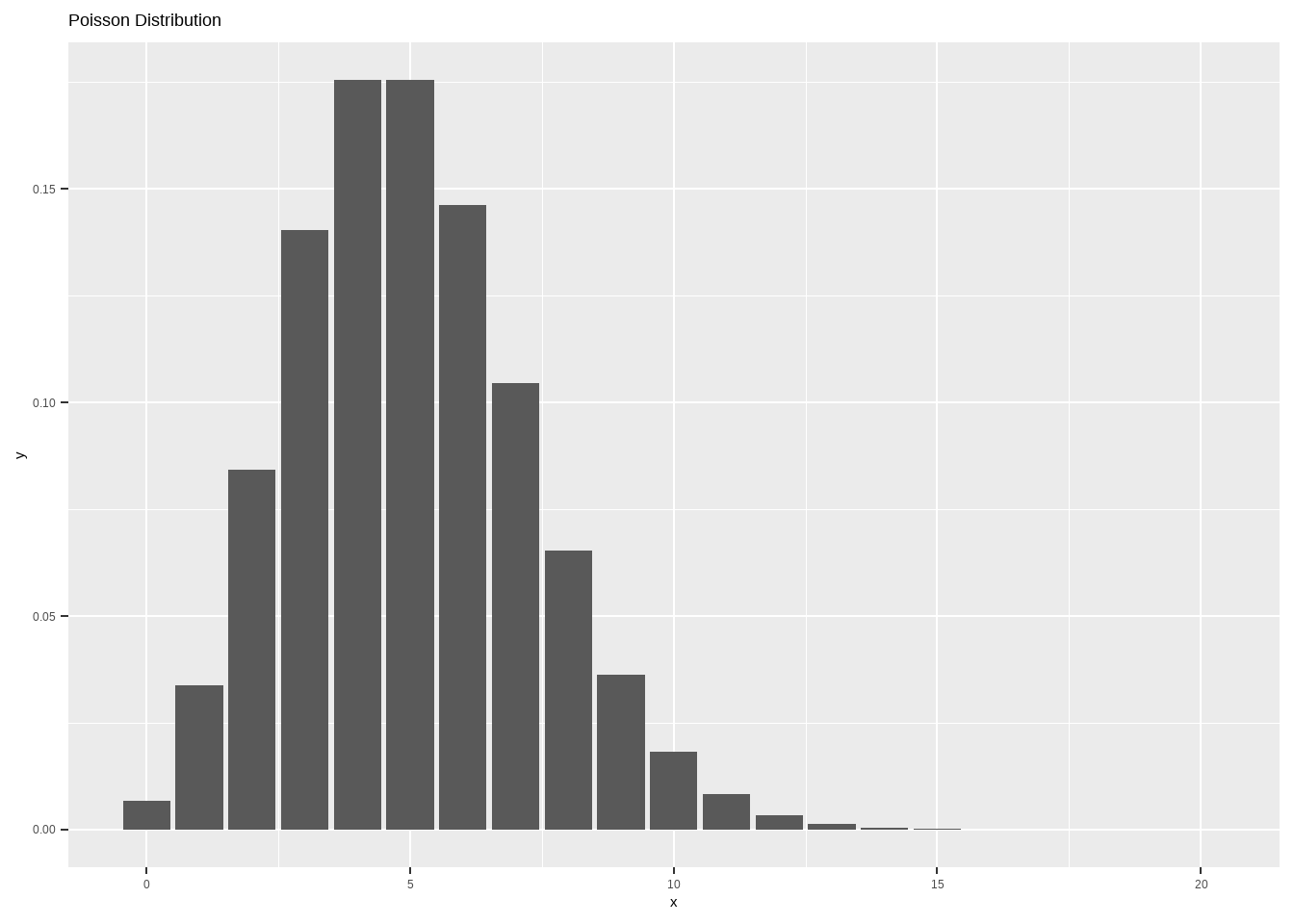
\[ P(x)=\frac{\lambda^x e^{-\lambda}}{x!}，E(X)=Var(X)=λ \]

# 泊松分布
poisson_data <- tibble(x = 0:20,
                       y = dpois(x, lambda = 5))

ggplot(poisson_data, aes(x = x, y = y)) +
    geom_col() +
    ggtitle("Poisson Distribution")

4. 超几何分布：Hypergeometric Distribution，不放回抽样 ， Fisher’s Exact Test

\[ P(x)=\frac{\binom {m}{x}\binom{n}{k-x}}{\binom{m+n}{k}}；x=0，...，k；p=m/(m+n) ；N=m+n \]

其中，\(p = \frac{m}{m+n}\)，\(N = m+n\)，均值 \(E[X] = \mu = kp\)，方差 \(Var(X) = kp(1-p) \frac{(m+n-1)}{(m+n-k)}\)。

# 超几何分布
hypergeometric_data <- tibble(x = -10:10, y = dhyper(x, m = 10,n = 7,k = 8))

ggplot(hypergeometric_data, aes(x = x, y = y)) +
    geom_bar(stat = "identity") +
    ggtitle("Hypergeometric Distribution")

5. 多项式分布

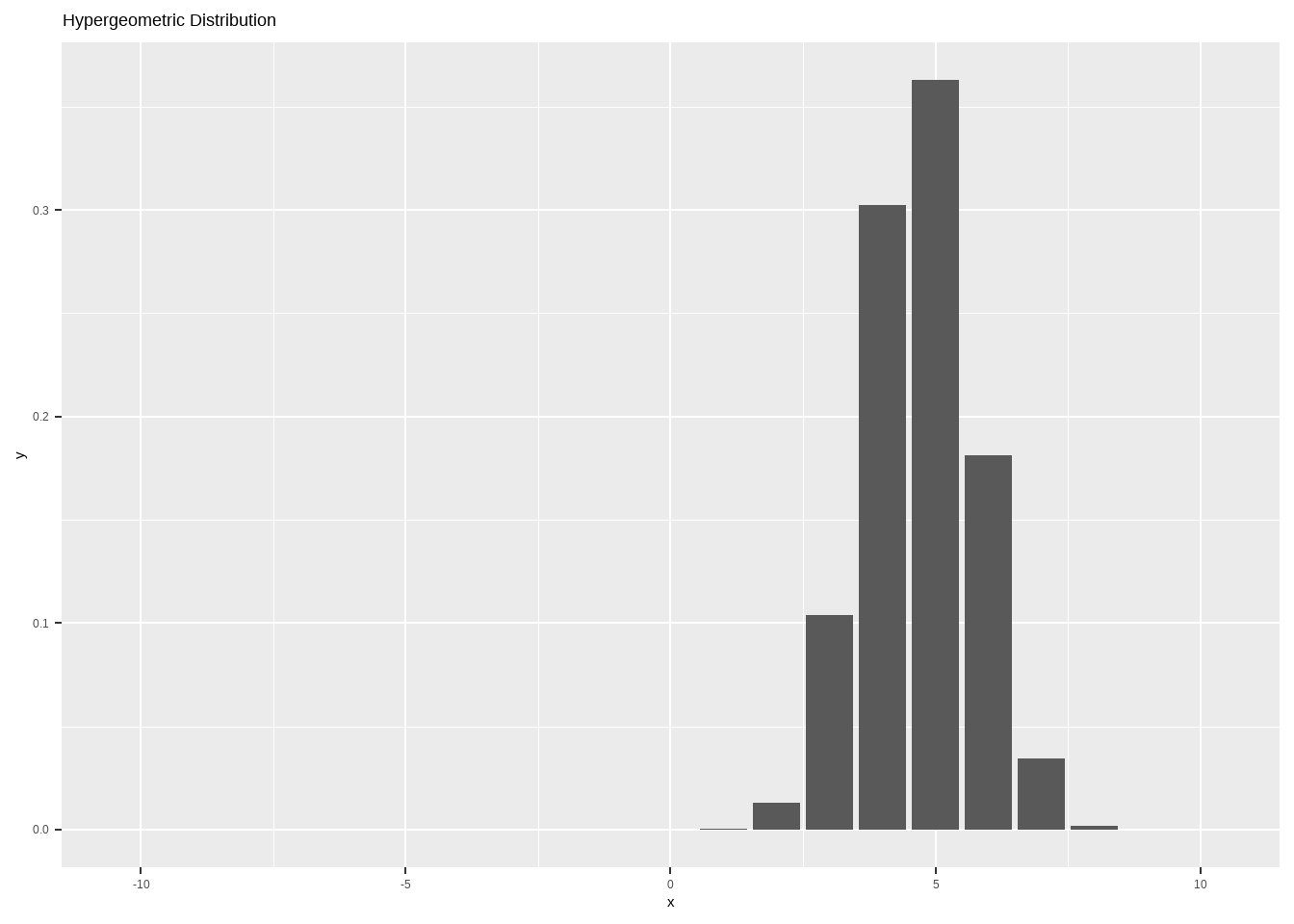
DNA [ A, G, C, T ]

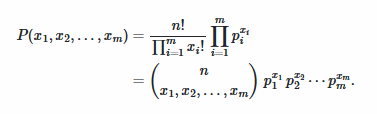
假设我们有四个可能性相等的框。使用公式，在第一个框中观察到 4，在第二个框中观察到 2，而在其他两个框中没有观察到的概率是多少？

dmultinom(c(4, 2, 0, 0), prob = rep(1/4, 4))
#> [1] 0.003662109

定性数据（qualitative data）

名义型（nominal）

有序型（ordered）

数据可视化