20 诊断性测试

Modified

November 20, 2024

20.1 混淆矩阵

Show the code

m<- matrix(c("TP","FN","FP","TN"),nrow = 2,
           dimnames = list(predict=c("+","-"),
                           truth=c("+","-")))
print(m)
#>        truth
#> predict +    -   
#>       + "TP" "FP"
#>       - "FN" "TN"

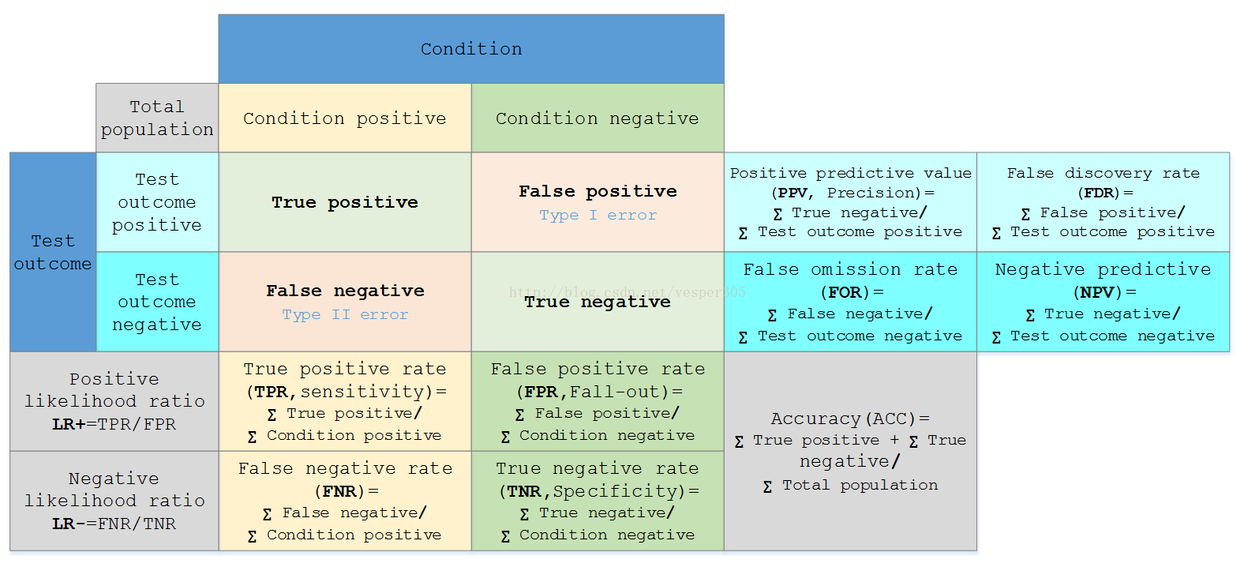
20.2 灵敏度（Sensitivity）

真阳性率：指在所有真实状况为阳性的样本中，被正确识别出阳性的比例。

\[ Se=\frac{TP}{TP+FN} \]

其中TP 是真阳性的数量，FN 是假阴性的数量。

20.2.1 假阴性率(FNR) /漏诊率

\[ FNR=1-Se \]

20.3 特异度（Specificity）

真阴性率：指在所有真实状况为阴性的样本中，被正确识别出阴性的比例。

\[ Sp=\frac{TN}{TN+FP} \]

其中 TN 是真阴性的数量，FP 是假阳性的数量。

20.3.1 假阳性率(FPR) /误诊率

\[ FPR=1-Sp \]

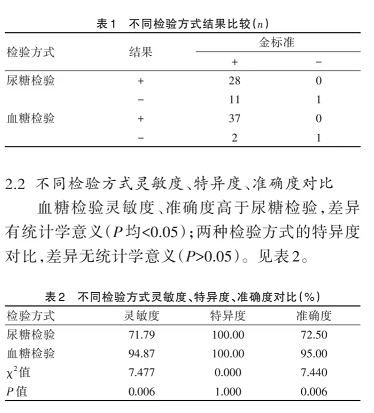
Show the code

# 构建列联表
observed_sensitivity <- matrix(c(28, 11, 37, 2), nrow = 2, byrow = TRUE,
                   dimnames = list('检验方式' = c('尿糖检验', '血糖检验'),
                                   '结果' = c('检出阳性', '未检出阳性')))
observed_sensitivity
#>           结果
#> 检验方式 检出阳性 未检出阳性
#>   尿糖检验       28         11
#>   血糖检验       37          2
# 进行卡方检验
s <- chisq.test(observed_sensitivity,correct = F)

# 输出结果
s
#> 
#>  Pearson's Chi-squared test
#> 
#> data:  observed_sensitivity
#> X-squared = 7.4769, df = 1, p-value = 0.006249


# 构建列联表
observed_accuracy <- matrix(c(29, 11, 38, 2), nrow = 2, byrow = TRUE,
                            dimnames = list('检验方式' = c('尿糖检验', '血糖检验'),
                                            '结果' = c('检准', '不准')))

# 进行卡方检验
accuracy <- chisq.test(observed_accuracy,correct = F)

# 输出结果
accuracy
#> 
#>  Pearson's Chi-squared test
#> 
#> data:  observed_accuracy
#> X-squared = 7.4397, df = 1, p-value = 0.00638

20.4 Youden’s Index

\[ J=Se-FPR =Se+Sp-1,J[1,-1] \]

J 越大诊断有效性越高
J=1 表示完美的诊断性能，因为Se，Sp都是1。
J≤0 表示没有诊断价值

20.5 Likelihood Ratio

20.5.1 正似然比

\[ LR+=\frac{Se}{FPR}=\frac{Se}{1-Sp} \]

LR+越大表示患病测出阳性结果的优势越大
LR+=1表示诊断无效

20.5.2 负似然比

\[ LR-=\frac{FNR}{Sp}=\frac{1-Sp}{Sp} \]

LR-越小表示患病测出阴性结果的优势越小
LR-=1表示诊断无效

20.6 预测值

Show the code

m
#>        truth
#> predict +    -   
#>       + "TP" "FP"
#>       - "FN" "TN"

阳性预测值（Positive Predictive Value, PPV）：在所有被测试为阳性的样本中，真正的阳性比例。

\[ PPV=\frac{TP}{TP+NP} \]

阴性预测值（Negative Predictive Value, NPV）：在所有被测试为阴性的样本中，真正的阴性比例。

\[ PPV=\frac{TN}{TN+FN} \]

配对样本设计

\(\chi^2\)配对检验

完全随机设计

\(\chi^2\)检验

20.7 一致性（agreement）

准确度（Accuracy）：指测试正确地分类（阳性或阴性）的样本占总样本的比例。

\[ Accuracy=\frac{TP+TN}{N} \]

kappa 系数

\[ \kappa =\frac{Accuracy-[(a+b)(a+c)+(c+d)(b+d)]/N^2}{1-[(a+b)(a+c)+(c+d)(b+d)]/N^2} \]

κ=1表示完全一致
κ=-1表示完全不一致
κ=0表示一致性与偶然一致性P_e相同

通常κ＞0.7即可以认为两种诊断方法有较好的一致性

20.8 ROC曲线（Receiver Operating Characteristic Curve）

ROC曲线（Receiver Operating Characteristic Curve）：是一个图形工具，用于展示不同阈值下灵敏度和特异度之间的关系。曲线下面积（AUC）越接近1，表示测试的性能越好。

Show the code

library(pROC)

roc_data <- aSAH %>%
    dplyr::filter(gender == "Female") %>%
    roc(outcome, s100b)



# 绘制ROC曲线
plot(roc_data, print.thres = "best", print.thres.pattern = "Best cutoff: %.2f", main = "ROC Curve")

Show the code



# 计算AUC
auc_value <- auc(roc_data)
print(paste("AUC:", auc_value))
#> [1] "AUC: 0.72"

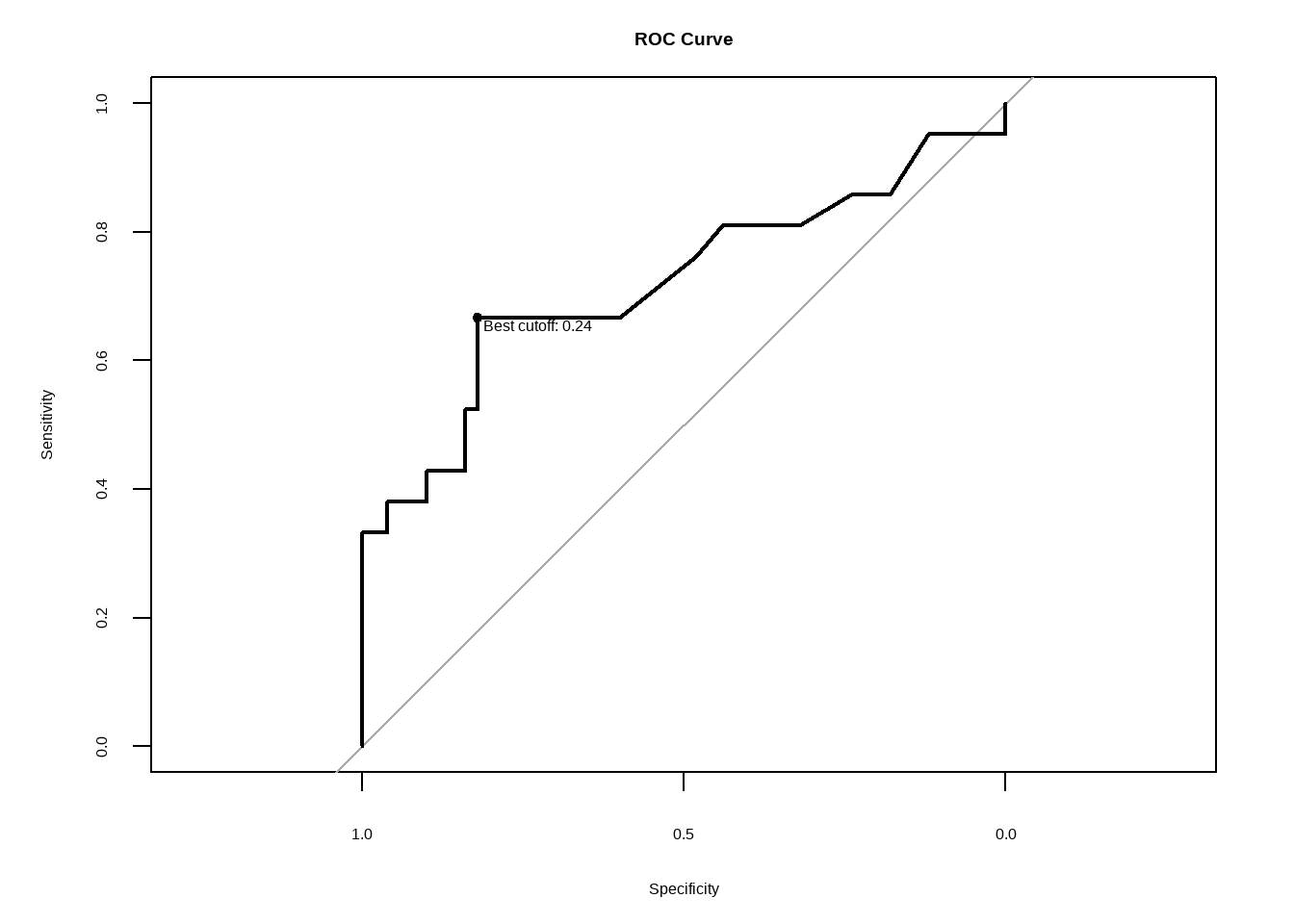
20.8.1 AUC

A=P(X>Y)

\[ S(X,Y)= \begin{cases} 1,\ \ \ \ X>Y\\ 1/2,X=Y\\ 0,\ \ \ \ X<Y\\ \end{cases} \]

\[ \hat A=\frac{1}{n_0n_1}\sum_1^{n1}\sum_1^{n_0}S(X, Y) \]

20.8.2 分组AUC的比较

完全随机设计

\[ Z=\frac{\hat A_1-\hat A_2}{\sqrt{Var(\hat A_1)+Var(\hat A_2)}} \]

配对样本设计

\[ Z=\frac{\hat A_1-\hat A_2}{\sqrt{Var(\hat A_1)+Var(\hat A_2)-2Cov(\hat A_1,\hat A_2)}} \]