11  非参数检验

Modified

November 20, 2024

11.1 秩

\[ F(Median)=P(X\le Median)=0.5 \]

Show the code
x <- c(1,4,2,2,6,9,5)
rank(x)
#> [1] 1.0 4.0 2.5 2.5 6.0 7.0 5.0

11.2 二项分布B(n，0.5)

Show the code
tibble(
    x = -5:15,
    y_binom = dbinom(x, size = 10,prob = 0.5),
) %>% 
ggplot()+
    geom_col(aes(x=x,y=y_binom,color="binomal Distribution"),fill=NA)+
    geom_function(mapping = aes(color="normal Distribution"),
                  fun = dnorm, args = list(mean = 5, sd = 1),
                   )+
    scale_color_manual(values = c("normal Distribution" = "red",
                                  "binomal Distribution" = "blue"))+
    labs(color = "Distribution")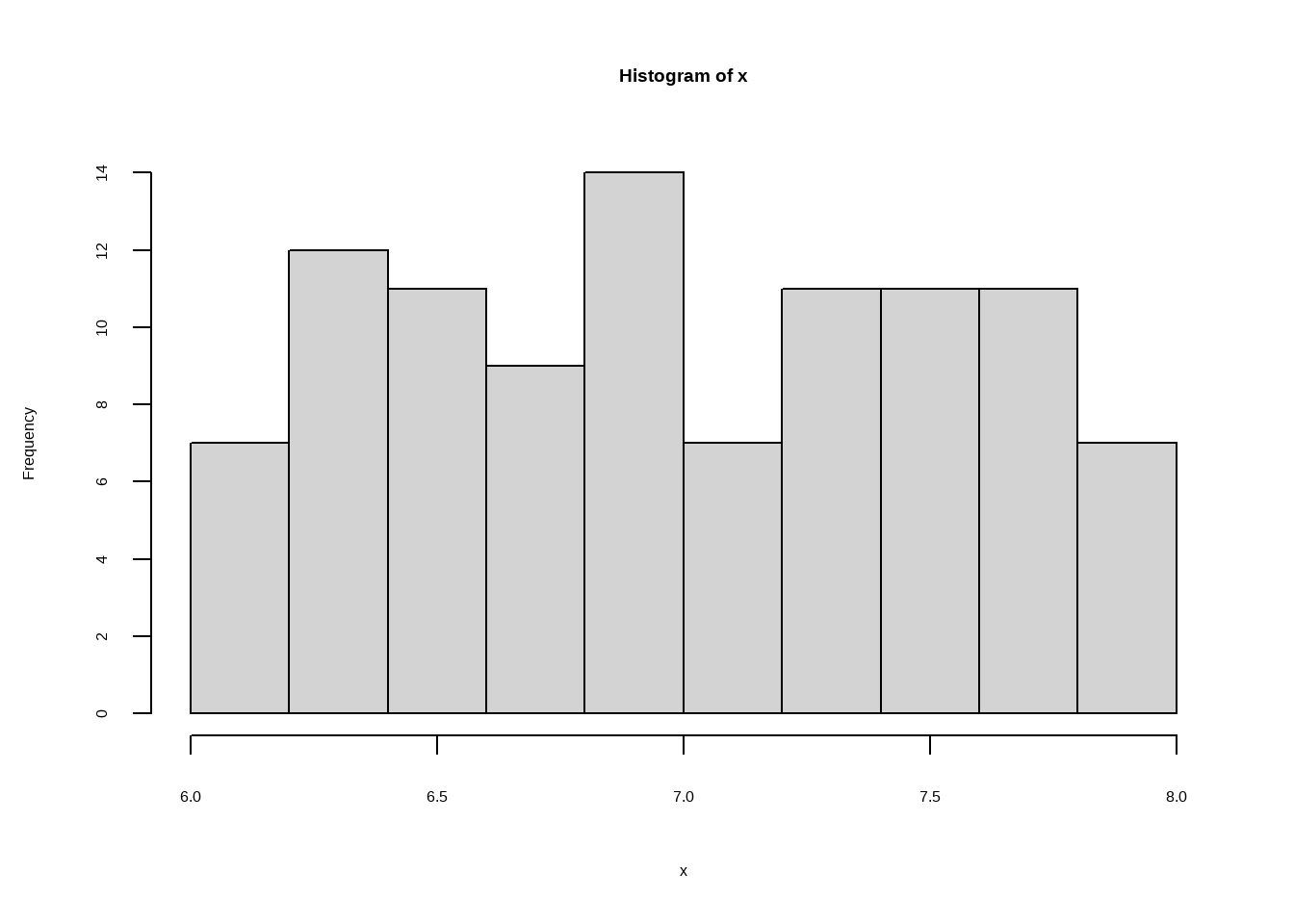

11.3 单样本 Wilcoxon Signed-Rank exact test

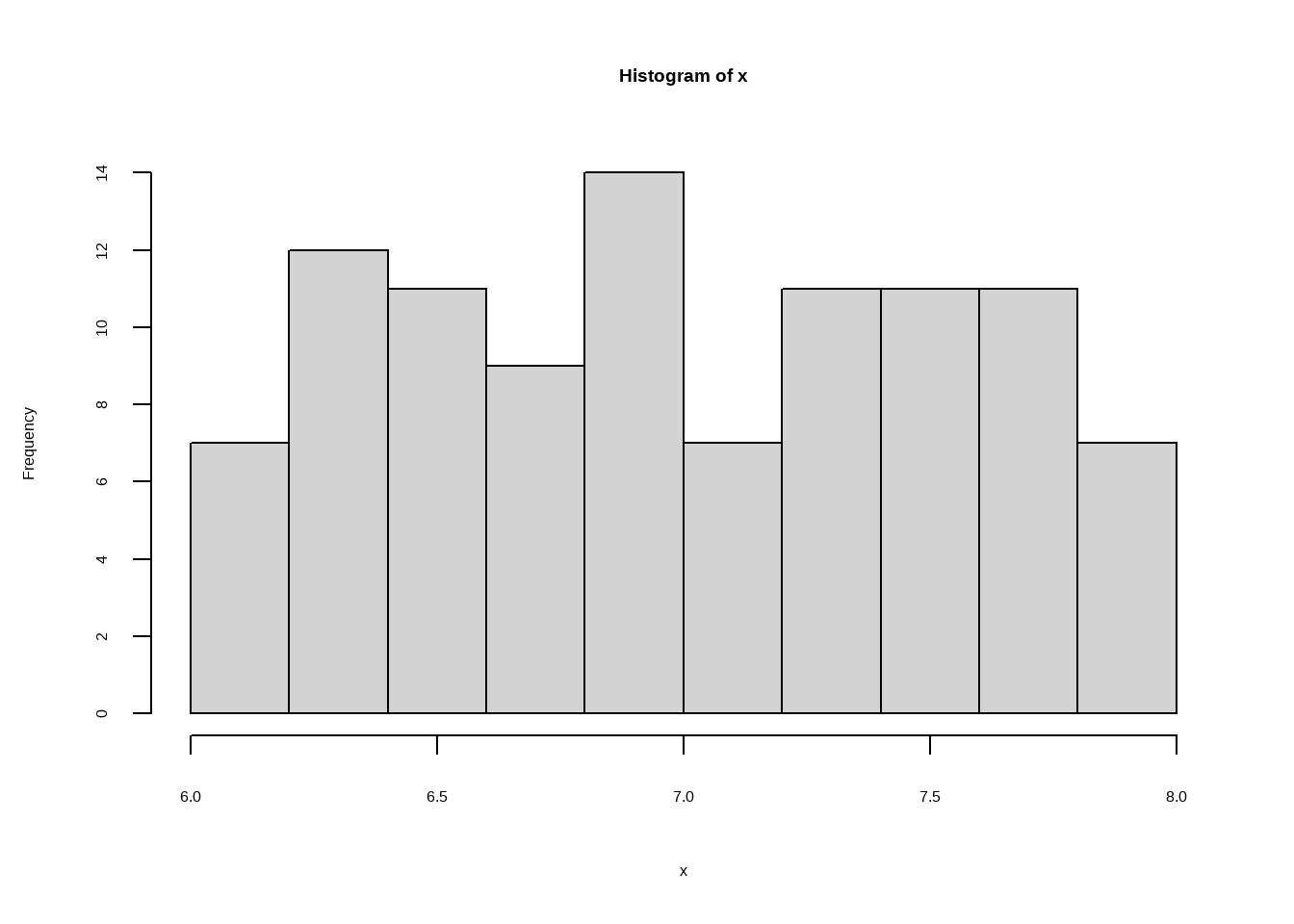
如果样本数据没有通过正态分布检验就要采用单样本wilcoxon符号秩检验进行计算。使用该检验需要满足的条件是样本值均匀地分布在均值两侧。

Show the code
set.seed(123)
x <- runif(n = 100,min = 6,max = 8)
hist(x)

Show the code
shapiro.test(x)
#> 
#>  Shapiro-Wilk normality test
#> 
#> data:  x
#> W = 0.95237, p-value = 0.001192
wilcox.test(x, mu=7) 
#> 
#>  Wilcoxon signed rank test with continuity correction
#> 
#> data:  x
#> V = 2518, p-value = 0.9822
#> alternative hypothesis: true location is not equal to 7

11.4 双样本

11.4.1 配对 Wilcoxon’s signed-rank test

\[ T_++T_-=\frac{n(n+1)}{2},n为非零配对差值的数量 \]

\[ T=min{(T_+,T_-)} \]

5 ≤ n ≤30，附表T0

n＞16，正态近似法

Show the code

df <- tibble(
    low=c(958.5,838.4,612.2,812.9,739.0,899.4,758.5,695.0,749.7,815.5),
    high=c(958.5,866.5,788.9,815.2,783.2,910.9,760.8,870.8,862.3,799.9),
)

shapiro.test(df$high-df$low)
#> 
#>  Shapiro-Wilk normality test
#> 
#> data:  df$high - df$low
#> W = 0.79689, p-value = 0.01329

# 忽略  差异绝对值为“0”的数剔除；
wilcox.test(df$low[-1],df$high[-1],exact = T,paired = T)
#> 
#>  Wilcoxon signed rank exact test
#> 
#> data:  df$low[-1] and df$high[-1]
#> V = 4, p-value = 0.02734
#> alternative hypothesis: true location shift is not equal to 0

11.4.2 独立 Wilcoxon’s Rank-Sum 检验 (Mann-Whitney U 检验)

当两个样本不满足正态分布时，使用Wilcoxon秩和检验进行非参数检验

用于比较两个独立样本的中位数是否相等。

\[ Wilxoxon秩和\ T=min\{T_1,T_2\} \]

Show the code
MVR = c(38, 29, 35, 33, 38, 41, 31)
MVP = c(32, 43, 44, 81, 35, 46, 37, 45, 44)
shapiro.test(c(MVR,MVP))
#> 
#>  Shapiro-Wilk normality test
#> 
#> data:  c(MVR, MVP)
#> W = 0.70443, p-value = 0.0001889

combined_data <- c(MVR, MVP)
ranked_data <- rank(combined_data)
ranked_data 
#>  [1]  8.5  1.0  5.5  4.0  8.5 10.0  2.0  3.0 11.0 12.5 16.0  5.5 15.0  7.0 14.0
#> [16] 12.5

MVR_ranks <- ranked_data[1:length(MVR)]
MVP_ranks <- ranked_data[(length(MVR)+1):length(combined_data)]

T1 <- sum(MVR_ranks)
T2 <- sum(MVP_ranks)

T1-length(MVR)*(length(MVR)+1)/2
#> [1] 11.5
wilcox.test(MVR,MVP,exact = F,correct = F)
#> 
#>  Wilcoxon rank sum test
#> 
#> data:  MVR and MVP
#> W = 11.5, p-value = 0.03386
#> alternative hypothesis: true location shift is not equal to 0

11.4.2.1 W统计量

n1<10,n2-n1<10，附录

n1>10,n2>10，正态近似法

Show the code
x <- c(17, 12, 13, 16, 9, 19, 21, 12, 18, 17)
y <- c(10, 6, 15, 9, 8, 11, 8, 16, 13, 7, 5, 14)
wilcox.test(x, y, correct = F)
#> 
#>  Wilcoxon rank sum test
#> 
#> data:  x and y
#> W = 101.5, p-value = 0.006124
#> alternative hypothesis: true location shift is not equal to 0

rank(c(x,y))[1:10] %>% sum()
#> [1] 156.5
rank(c(x,y))[11:22] %>% sum()
#> [1] 96.5

156.5-10*11/2
#> [1] 101.5

a <- wilcox.test(x,y,correct=FALSE)
str(a) 
#> List of 7
#>  $ statistic  : Named num 102
#>   ..- attr(*, "names")= chr "W"
#>  $ parameter  : NULL
#>  $ p.value    : num 0.00612
#>  $ null.value : Named num 0
#>   ..- attr(*, "names")= chr "location shift"
#>  $ alternative: chr "two.sided"
#>  $ method     : chr "Wilcoxon rank sum test"
#>  $ data.name  : chr "x and y"
#>  - attr(*, "class")= chr "htest"
n1 <- length(x)
a$statistic <- a$statistic + n1*(n1+1)/2
names(a$statistic) <- "T.W"
a
#> 
#>  Wilcoxon rank sum test
#> 
#> data:  x and y
#> T.W = 156.5, p-value = 0.006124
#> alternative hypothesis: true location shift is not equal to 0

11.4.2.2 曼-惠特尼 U 统计量

\[ 曼-惠特尼U统计量= 威尔科克森W(较小秩和)-\frac{n_{T_{min}}(n_{T_{min}}+1)}{2} \]

11.4.2.3 Z 统计量 coin::wilcox_test()

Show the code
library(coin)
df <- read_excel("data/coin-wilcox_test.xlsx") %>% 
    mutate(group=as.factor(group))
df
#> # A tibble: 240 × 2
#>    HADS得分 group
#>       <dbl> <fct>
#>  1       14 1    
#>  2       14 1    
#>  3        7 1    
#>  4       22 1    
#>  5        7 1    
#>  6       12 1    
#>  7       15 1    
#>  8       17 1    
#>  9        8 1    
#> 10       14 1    
#> # ℹ 230 more rows

rank <- rank(df$HADS得分)

g1rankSum <- sum(rank[1:120])
g2rankSum <- sum(rank[121:240])


SPSS_威尔科克森W <- min(g1rankSum,g2rankSum)
SPSS_威尔科克森W 
#> [1] 13965.5
SPSS_曼惠特尼U <-  SPSS_威尔科克森W -120*121/2
SPSS_曼惠特尼U
#> [1] 6705.5

wilcox.test(HADS得分 ~ group,data=df,correct=F)
#> 
#>  Wilcoxon rank sum test
#> 
#> data:  HADS得分 by group
#> W = 7694.5, p-value = 0.3572
#> alternative hypothesis: true location shift is not equal to 0
# SPSS  z统计量
coin::wilcox_test( HADS得分 ~ group,data=df, distribution = "asymptotic") #   exact   asymptotic    approximate
#> 
#>  Asymptotic Wilcoxon-Mann-Whitney Test
#> 
#> data:  HADS得分 by group (1, 2)
#> Z = 0.92062, p-value = 0.3572
#> alternative hypothesis: true mu is not equal to 0
coin::wilcox_test( HADS得分 ~ group,data=df, distribution = "approximate")
#> 
#>  Approximative Wilcoxon-Mann-Whitney Test
#> 
#> data:  HADS得分 by group (1, 2)
#> Z = 0.92062, p-value = 0.3589
#> alternative hypothesis: true mu is not equal to 0

SPSS 用较小秩和减去对应 n(n+1)/2

R有时用较小秩和减去对应 n(n+1)/2，有时用较大秩和减去对应 n(n+1)/2

Show the code
wilcox.test(HADS得分 ~ group,data=df,exact = F,correct = F)
#> 
#>  Wilcoxon rank sum test
#> 
#> data:  HADS得分 by group
#> W = 7694.5, p-value = 0.3572
#> alternative hypothesis: true location shift is not equal to 0

# SPSS_曼惠特尼U
g2rankSum-120*121/2
#> [1] 6705.5


# R中W
g1rankSum-120*121/2
#> [1] 7694.5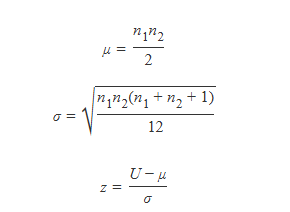

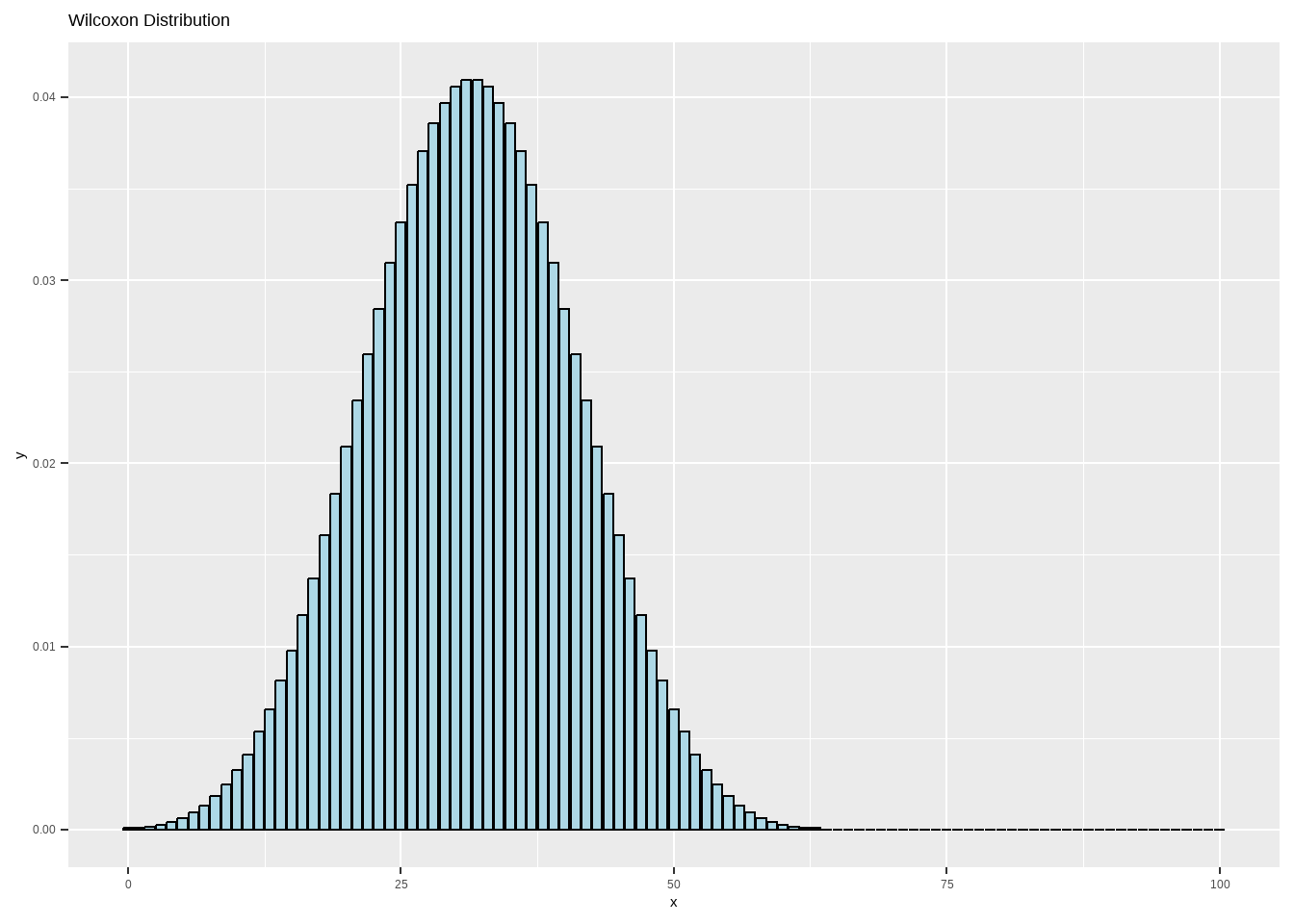
n1>20

11.4.3 Wilcoxon Distribution

Show the code

tibble(
    x = 0:100,
    y =dwilcox(x,m = 7,n = 9)
) %>% 
    ggplot() +
    geom_col(aes(x,y),fill="lightblue",color="black")+
    ggtitle("Wilcoxon Distribution")

11.5 多样本

11.5.1 独立 Kruskal-Wallis 检验

用于比较三个或更多独立样本的中位数是否相等。

假设：

  1. 随机，独立

  2. 每个样本至少5个观测

  3. 能够计算秩次

Show the code
kruskal.test(weight~group,data = PlantGrowth)
#> 
#>  Kruskal-Wallis rank sum test
#> 
#> data:  weight by group
#> Kruskal-Wallis chi-squared = 7.9882, df = 2, p-value = 0.01842

11.5.1.1 事后多重比较

Show the code
pairwise.wilcox.test(PlantGrowth$weight,PlantGrowth$group,p.adjust.method = "fdr",exact=F)
#> 
#>  Pairwise comparisons using Wilcoxon rank sum test with continuity correction 
#> 
#> data:  PlantGrowth$weight and PlantGrowth$group 
#> 
#>      ctrl  trt1 
#> trt1 0.199 -    
#> trt2 0.096 0.034
#> 
#> P value adjustment method: fdr

11.5.2 相关 Friedman 检验

用于比较三个或更多相关样本的中位数是否相等。

Show the code
# 假设有三个相关样本 x, y, z
x <- c(14, 17, 20, 23, 25)
y <- c(15, 18, 21, 24, 26)
z <- c(16, 19, 22, 25, 27)

# 将样本合并成一个数据框，并指定组别和受试者
data <- data.frame(
  value = c(x, y, z),
  group = factor(rep(c("x", "y", "z"), each = 5)),
  subject = factor(rep(1:5, 3))
)

# 使用 friedman.test() 函数进行检验
result <- friedman.test(value ~ group | subject, data = data)

# 输出检验结果
print(result)
#> 
#>  Friedman rank sum test
#> 
#> data:  value and group and subject
#> Friedman chi-squared = 10, df = 2, p-value = 0.006738

11.6 Kendall’s Tau 检验

用途：用于检验两个变量之间的相关性。

Show the code
# 假设有两个变量 x 和 y
x <- c(14, 17, 20, 23, 25)
y <- c(15, 18, 21, 24, 26)

# 使用 cor.test() 函数进行 Kendall's Tau 检验
result <- cor.test(x, y, method = "kendall")

# 输出检验结果
print(result)
#> 
#>  Kendall's rank correlation tau
#> 
#> data:  x and y
#> T = 10, p-value = 0.01667
#> alternative hypothesis: true tau is not equal to 0
#> sample estimates:
#> tau 
#>   1

11.7 Spearman’s Rank Correlation 检验

用途：用于检验两个变量之间的相关性，适用于数据非线性关系。

Show the code
# 假设有两个变量 x 和 y
x <- c(14, 17, 20, 23, 25)
y <- c(15, 18, 21, 24, 26)

# 使用 cor.test() 函数进行 Spearman's Rank Correlation 检验
result <- cor.test(x, y, method = "spearman")

# 输出检验结果
print(result)
#> 
#>  Spearman's rank correlation rho
#> 
#> data:  x and y
#> S = 4.4409e-15, p-value = 0.01667
#> alternative hypothesis: true rho is not equal to 0
#> sample estimates:
#> rho 
#>   1