Cox比例风险模型是一种半参数方法
风险函数
\[
\begin{aligned}
h(t)=&\lim_{\Delta t\to 0}\frac{P(t\le T<t+\Delta t|T\ge t)}{\Delta t}\\
=&\lim_{\Delta t\to 0}\frac{P(t\le T<t+\Delta t\ \&\ T\ge t)}{\Delta t·P(T\ge t) }\\
=&\lim_{\Delta t\to 0}\frac{S(t)- S(t+\Delta t)}{\Delta t·S(t)}\\
=&-\frac{d(\ln S(t))}{dt}
\end{aligned}
\]
推导出 \(S(t)=e^{-\int_0^t h(u)du}\)
\[
\begin{aligned}
h(t)\Delta t=&P(t\le T<t+\Delta t|T\ge t)
=\frac{P(t\le T<t+\Delta t\ \&\ T\ge t)}{P(T\ge t) }\\
=&\frac{P(t\le T<t+\Delta t)}{P(T\ge t) }\\
=&\frac{f(t)\Delta t}{S(t)}
\end{aligned}
\]
推导出 \(f(t)=h(t)S(t)\)
风险率
对于有风险因子\(x_1,x_2,...,x_k\) 的个体在时间 t 的风险率\(h(t|x_1,x_2,...,x_k)\)
\[ h(t|x_1,x_2,...,x_k)=h_0(t)g(x_1,x_2,...,x_k)=h_0(t)exp(\sum_{j=1}^k\beta_jx_j) \]
其中
\(h0 (t)\)是给定所有风险因子(协变量)为零的随时间变化的基线风险函数。
\(g(X)\)是k个独立风险因子的集合函数,代表变量的风险效应。
\(β_j\)是部分回归系数,表示风险比的比例变化。
风险比(hazard ratio)
假设有两个个体,分别具有独立变量,两个个体的风险函数之比称为风险比
\[ HR=\frac{h(t|x_1,x_2,...,x_k)}{h(t|x_1^*,x_2^*,...,x_k^*)}=exp(\sum_{j=1}^k\beta_j(x_j-x_j^*)) \]
比例风险假设(proportional hazards assumption)
Cox 模型假设任意两组之间的 HR 随时间保持不变
\[ \frac{h(t)}{h_0(t)}=exp(\sum_{j=1}^k\beta_jx_j) \]
模型系数的估计
条件死亡概率和局部似然函数方法
\[ \ln L_p(\beta)=\sum_{i=1}^{d}\left[ \sum_{j=1}^k\beta_jx_{ij}-\ln\sum_{m\in R_i}exp( \sum_{j=1}^k\beta_jx_{mj}) \right] \]
Newton-Raphson iterative method
\[ \begin{cases} \frac{\partial \ln L_p(\beta)}{\partial \beta_1}=0\\ \frac{\partial \ln L_p(\beta)}{\partial \beta_2}=0\\ \vdots\\ \frac{\partial \ln L_p(\beta)}{\partial \beta_k}=0\\ \end{cases} \]
模型系数的假设检验
-
Wald‘s test
检验是否有独立变量需要被消除,统计量\(Z=b_j/S_{b_j}\)
当样本量足够大时,Z服从标准正态分布,Z2 服从自由度为1 的\(\chi^2\) 分布
\[ \chi^2_W=(b_j/S_{b_j})^2\sim \chi^2(1) \]
-
Partial likelihood Ratio test
主要用于非显著性变量的消除,新变量的引入和模型的比较。
\[ \chi^2_{LR}=2\left[ \ln L_p(\beta_k)-\ln L_p(\beta_{k-1}) \right]\sim\chi^2(1) \]
其中分别是包含 k 个和 k-1 个(不包含要检验的第 j 个变量)独立变量的对数局部似然函数
示例
Show the code
library(survminer)
library(survival)
df <- survival::rotterdam
df <- df %>% mutate(dtime_yrs = dtime/365.25,
status = death)
# 拟合Cox比例风险模型
cox_model <- coxph(Surv(dtime_yrs, status) ~ hormon + chemo + size + er + pgr + nodes + meno + grade + age, data = df)
# 查看模型结果
summary(cox_model)
#> Call:
#> coxph(formula = Surv(dtime_yrs, status) ~ hormon + chemo + size +
#> er + pgr + nodes + meno + grade + age, data = df)
#>
#> n= 2982, number of events= 1272
#>
#> coef exp(coef) se(coef) z Pr(>|z|)
#> hormon -6.553e-02 9.366e-01 8.840e-02 -0.741 0.458535
#> chemo 5.032e-02 1.052e+00 8.198e-02 0.614 0.539342
#> size20-50 4.425e-01 1.557e+00 6.536e-02 6.771 1.28e-11 ***
#> size>50 8.222e-01 2.276e+00 9.142e-02 8.993 < 2e-16 ***
#> er -5.512e-05 9.999e-01 1.107e-04 -0.498 0.618466
#> pgr -3.676e-04 9.996e-01 1.226e-04 -2.998 0.002720 **
#> nodes 7.295e-02 1.076e+00 4.879e-03 14.953 < 2e-16 ***
#> meno 7.046e-02 1.073e+00 1.006e-01 0.701 0.483583
#> grade 3.156e-01 1.371e+00 7.082e-02 4.456 8.33e-06 ***
#> age 1.406e-02 1.014e+00 3.830e-03 3.671 0.000242 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> exp(coef) exp(-coef) lower .95 upper .95
#> hormon 0.9366 1.0677 0.7876 1.1137
#> chemo 1.0516 0.9509 0.8955 1.2349
#> size20-50 1.5567 0.6424 1.3695 1.7694
#> size>50 2.2755 0.4395 1.9022 2.7221
#> er 0.9999 1.0001 0.9997 1.0002
#> pgr 0.9996 1.0004 0.9994 0.9999
#> nodes 1.0757 0.9296 1.0654 1.0860
#> meno 1.0730 0.9320 0.8810 1.3068
#> grade 1.3711 0.7293 1.1934 1.5753
#> age 1.0142 0.9860 1.0066 1.0218
#>
#> Concordance= 0.693 (se = 0.008 )
#> Likelihood ratio test= 524.4 on 10 df, p=<2e-16
#> Wald test = 609.4 on 10 df, p=<2e-16
#> Score (logrank) test = 688.1 on 10 df, p=<2e-16
例如,与未接受激素治疗的患者相比,在任何给定时间接受激素治疗患者的结局(死亡)概率为0.9366。换句话说,他们的生存率提高了6.34%。对于每个组,我们比较了该特征的存在(=1)和不存在(=0)。例如,对于激素治疗,我们有2600名患者没有接受激素治疗,而300名患者接受了激素治疗。因此,系数是指接受治疗与不接受治疗的对数风险率的变化,换句话说,“不接受激素治疗”组是我们的参考。
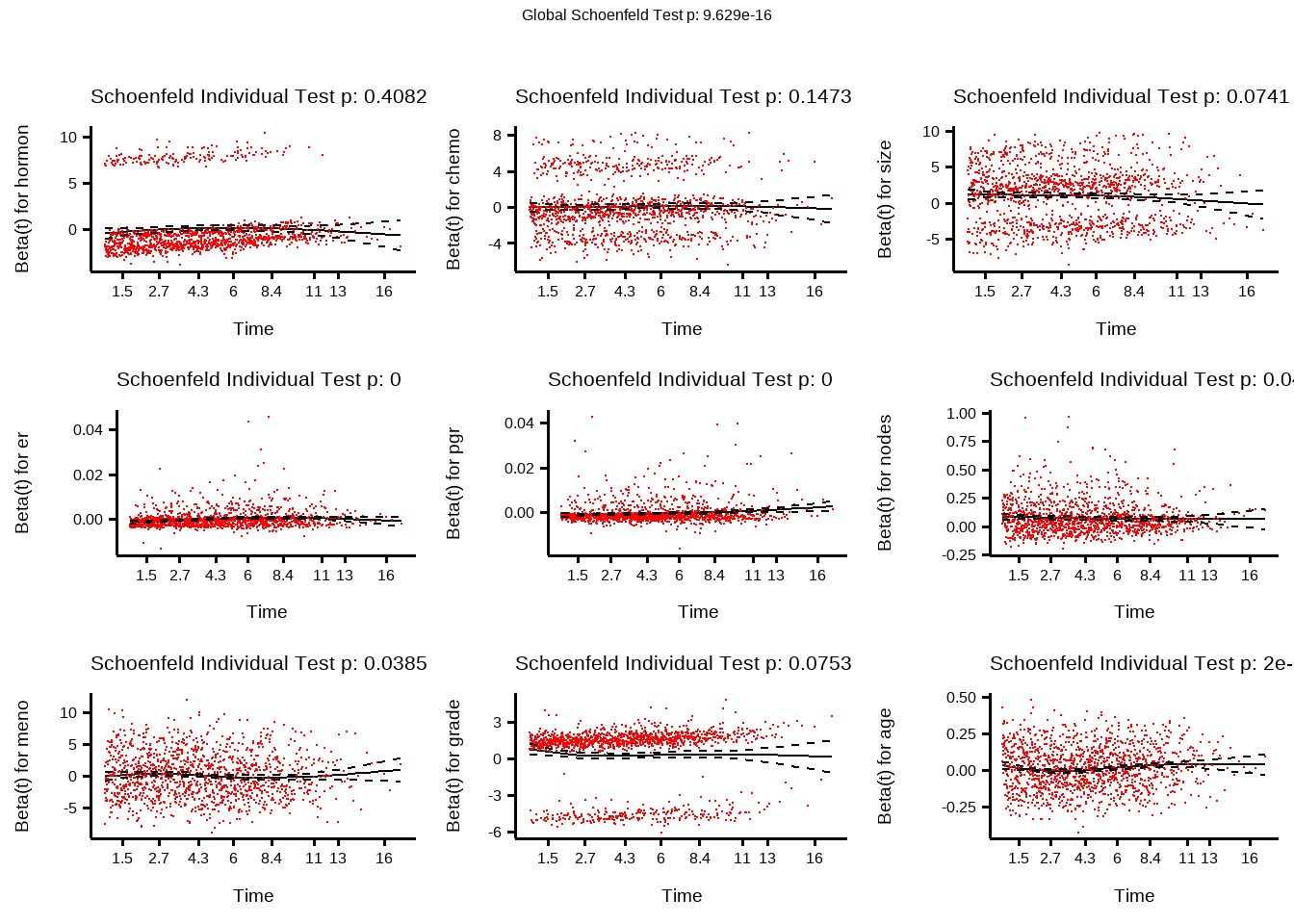
在解释 Cox regresison 的结果之前,请验证是否遵循比例风险假设。
Cox 模型假设任意两组之间的 HR 随时间保持不变。我们可以使用 cox.zph() 非常轻松地对其进行测试。
Show the code
test <- survival::cox.zph(cox_model)
test
#> chisq df p
#> hormon 0.684 1 0.40818
#> chemo 2.100 1 0.14727
#> size 5.206 2 0.07405
#> er 59.748 1 1.1e-14
#> pgr 41.637 1 1.1e-10
#> nodes 4.073 1 0.04358
#> meno 4.284 1 0.03846
#> grade 3.163 1 0.07533
#> age 13.954 1 0.00019
#> GLOBAL 93.751 10 9.6e-16
基于Schoenfeld residuals 的比例风险假设
Show the code
# 绘制每个协变量随时间变化的 Schoenfeld 残差
survminer::ggcoxzph(test, point.size = 0.1)
如果残差随时间显示清晰的模式,则可能表示违反了比例风险假设。
一些有助于解释的提示:
无模式(常数残差):如果残差随机分布在零附近,没有明确的趋势或模式,则表明比例风险假设是合理的:)
线性趋势:残差随时间变化的线性趋势(增加或减少)可能表明违反了比例风险假设。例如,如果残差在一段时间内始终为正或负,则表示存在时间相关效应。
非线性模式:如果残差表现出非线性模式或特定形状(例如,U 形、V 形),则可能表示偏离比例风险。
并行度:平行度意味着残差的分布和分布在时间上相对恒定。如果残差随时间变宽或变窄,则可能表明违反了假设。