Code
# 假设随机试验是抛掷硬币
w1 <- "正面"
w2 <- "反面"样本点(sample point)是每一次随机试验的结果,用 \(\omega\) 表示。
# 假设随机试验是抛掷硬币
w1 <- "正面"
w2 <- "反面"样本空间(sample space)是所有样本点的集合,用\(\Omega=\{\omega_{i};i=0,1,2,... \}\)表示。
space<- c(w1=w1,w2=w2)
space
#> w1 w2
#> "正面" "反面"随机事件(random event)是样本空间中满足一定条件的子集(\(\Omega\)的子集),用大写字母 \(A,B,C,...\)表示。
一个样本点的集合称为简单事件(simple event),用 \(\Omega=\{\omega\}\) 表示。
若干个简单事件的集合称为混合事件(composite event)。
全集 \(\Omega\) 称为必然事件(deterministic event)。
空集(null set) \(\emptyset\) 称为不可能事件(impossible event)。
包含关系(containment) :Venn diagram
\(A\subseteq B\)
\(A\supseteq B\)
并集(\(A\cup B\))
交集(\(A\cap B\),\(AB\) )
补集(\(\bar A\))
互斥事件 \(A\cap B=\emptyset\)
对立(互补)事件 \(A\cap B=\emptyset\) 且 \(A\cup B=\Omega\)
组合(combination):\(C_n^k =\binom{n}{k} =\frac {n!}{k!(n-k)!}\)
choose(5,3)
#> [1] 10排列(permutation):\(P_n^k =k!\binom{n}{k} =\frac {n!}{(n-k)!}\)
加法定理
\[ P(A\cup B)=P(A)+P(B)-P(A\cap B) \]
条件概率 conditional probability
\[ P(B|A)=\frac{P(AB)}{P(A)} \]
推出乘法定理 \(P(A B)=P(A)\times P(B|A)\)
独立性(积的概率等于各自概率的积)
\[ P(B|A)=P(B) \ 或者\ P(A)=0\\ P(AB)=P(A) \times P(B) \]
(给定Ai发生,B的加权平均条件概率)
\[P(B)=\sum_{i=1}^{n}P(A_i)P(B|A_i)\]
条件概率定义与全概率公式的推论
逆概率公式(后验概率)
\[P(A_k |B)=\frac{P(A_k)P(B|A_k)}{\sum_{i=1}^{n}P(A_i)P(B|A_i)}\]
离散型随机变量的全部可能取值只有有限多个或可列无穷多个。
离散型随机变量的概率分布列:
\[P(X=x_k)=p_k \ ,\ \ (k=1,2,…)\]
累计分布函数:
\[F(x) =P(X≤x)= \sum_{x_k≤x}p_k\]
随机变量的数学期望或均值:
\[E(X)=\sum_{k}x_k p_k\ ,\ \ (k=1,2,...)\]
方差:
\[Var(X)=\sum_{k}(x_k-\mu)^2 p_k\]
二项试验
\[ X\sim B(n,\pi) \]
概率质量函数(pmf):
\[P(X=k)=p_k=C_n^k\pi^k(1-\pi)^{n-k} \ ,\ \ (k=0,1,...,n)\]
其中n表示独立试验的次数,\(\pi\) 表示成功概率。
累计概率:至多k0次成功的概率
\[F(X)=P(X≤k_0)=\sum_{k=0}^{k_0} p_k\]
至少k0次成功的概率
\[P(X≥k_0)=\sum_{k=k_0}^{n} p_k\]
期望:\(E(X)=n\pi\)
方差:\(Var(X)=n\pi(1-\pi)\)
binom <- function(n,p){
ggplot() +
geom_line(data.frame(x = 0:n,
y = dbinom(0:n, size = n, prob = p)),
mapping=aes(x = x, y = y),
color="red")+
geom_line(data.frame(x = 0:n,
y = pbinom(0:n, size = n, prob = p)),
mapping=aes(x = x, y = y),
color="blue")
}
binom(30,0.5)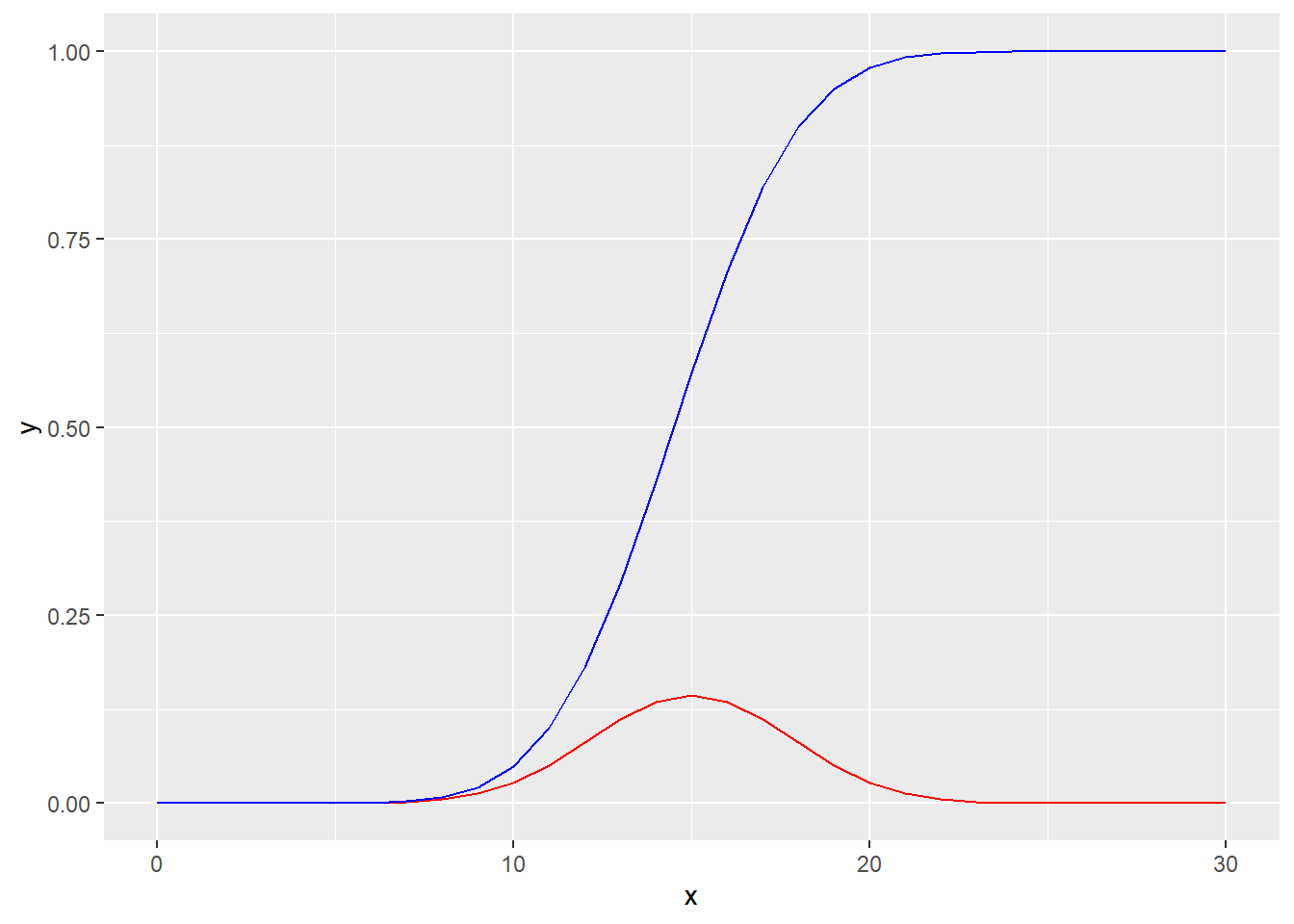
概率分布律:
\[P(X=k)=p_k=\frac {\binom{r}{k}\binom{N-r}{n-k}}{\binom{N}{n}} \ ,\ \ (k=0,1,...,r)\]
r为N中表示合格的元素个数,N-r表示不合格的元素个数,超几何分布考虑在n次无放回的试验中,k个合格n-k个不合格的概率。
期望:\(E(X)=\frac{nr}{N}\)
概率:\(P(X_1=n_1,...,X_i=n_i,...,X_k=n_k)=\frac {n!}{n_1!...n_i!...n_k!}\pi_1^{n_1}...\pi_i^{n_i}...\pi_k^{n_k}\)
\[ X \sim M(n,\pi_1,\pi_2,...,\pi_k) \]
其中\(n=n_1+n_2+...+n_k\) 表示独立试验的次数,\(\pi_k\) 表示\(k\) 个互斥结果的成功概率。
期望(\(A_i 与 -A_i\)):\(\mu_{A_i}=n\pi_{A_i}\)
方差(\(A_i 与 -A_i\)):\(\sigma_{A_i}^2=n\pi_{A_i}(1-\pi_{A_i})\)
特定时间段或某空间段内事件发生的次数
\[ X\sim P(\lambda) \] 概率分布列:
\[P(X=k)=p_k=\frac {\lambda ^k}{k!}e^{-\lambda} \ ,\ \ (\lambda > 0;k=0,1,…)\]
其中\(\lambda\) 表示单位时间/空间罕见事件发生的期望值。
期望:\(\mu=\lambda\)
方差:\(Var(X)=\lambda\)
当\(n(n≥100)\)足够大,\(\pi(\pi ≤0.01)\) 足够小,二项分布的均值 \(n\pi\) 与方差\(n\pi(1-\pi)\approx n\pi\) 近似相等,此时的二项分布近似\(\lambda=n\pi\) 的泊松分布。
\[ P(X=k)=C_n^k \pi^k(1-\pi)^{n-k} \approx \frac{\lambda ^k}{k!}e^{-\lambda} \]
对于随机变量X,如果存在一个定义在(-∞,+∞)上的非负函数f(x),使得对于任意实数x,总有:累计分布函数(cdf):
\[F(x)=P(X≤x)=\int_{-\infty}^{x}f(t)dt\]
概率:\(P(a≤X≤b)=\int_{a}^{b}f(x)dx\)
概率密度函数(pdf):\(f(x)\)
期望:\(E(X)\equiv\mu =\int_{-\infty}^{+\infty}xf(x)dx\)
方差:\(Var(X)\equiv \int_{-\infty}^{+\infty}(x-\mu)^2f(x)dx\)
概率密度函数(pdf):\(f(x)=\frac {1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}(-\infty <x <+\infty)\)
累计分布函数(cdf):\(F(x)=P(X≤x)=\int_{-\infty}^{x}f(t)dt=\frac{1}{\sqrt{2\pi}\sigma}\int_{-\infty}^{x}e^{-\frac{(t-\mu)^2}{2\sigma^2}}dt\ (-\infty<x<+\infty)\)
\[ X \sim N(\mu,\sigma^2) \]
\[ Z=\frac {X-\mu}{\sigma} \sim \ N(0,1) \]
pdf:\(\varphi (z)=\frac{1}{\sqrt{2\pi}}e^{-\frac{z^2}{2}} (-\infty<z<+\infty)\)
cdf:\(\Phi(z)=P(Z≤z)=\int_{-\infty}^{z}\varphi (\nu )d\nu =\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{z}e^{-\frac{\nu^2}{2}}dt\ (-\infty<z<+\infty)\)
直方图:钟形分布(bell-shaped distribution)
mtcars$mpg
#> [1] 21.0 21.0 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 17.8 16.4 17.3 15.2 10.4
#> [16] 10.4 14.7 32.4 30.4 33.9 21.5 15.5 15.2 13.3 19.2 27.3 26.0 30.4 15.8 19.7
#> [31] 15.0 21.4
h<-hist(mtcars$mpg,breaks = 12)
x<-seq(min(mtcars$mpg),max(mtcars$mpg),by=0.001)
y<-dnorm(x,mean=mean(mtcars$mpg),sd=sd(mtcars$mpg)) #密度曲线 f(x)=(F(i)/n)/ΔXi
y<-y*diff(h$mids[1:2])*length(mtcars$mpg) # f(x)*ΔXi*n 正态分布
lines(x,y,col="blue")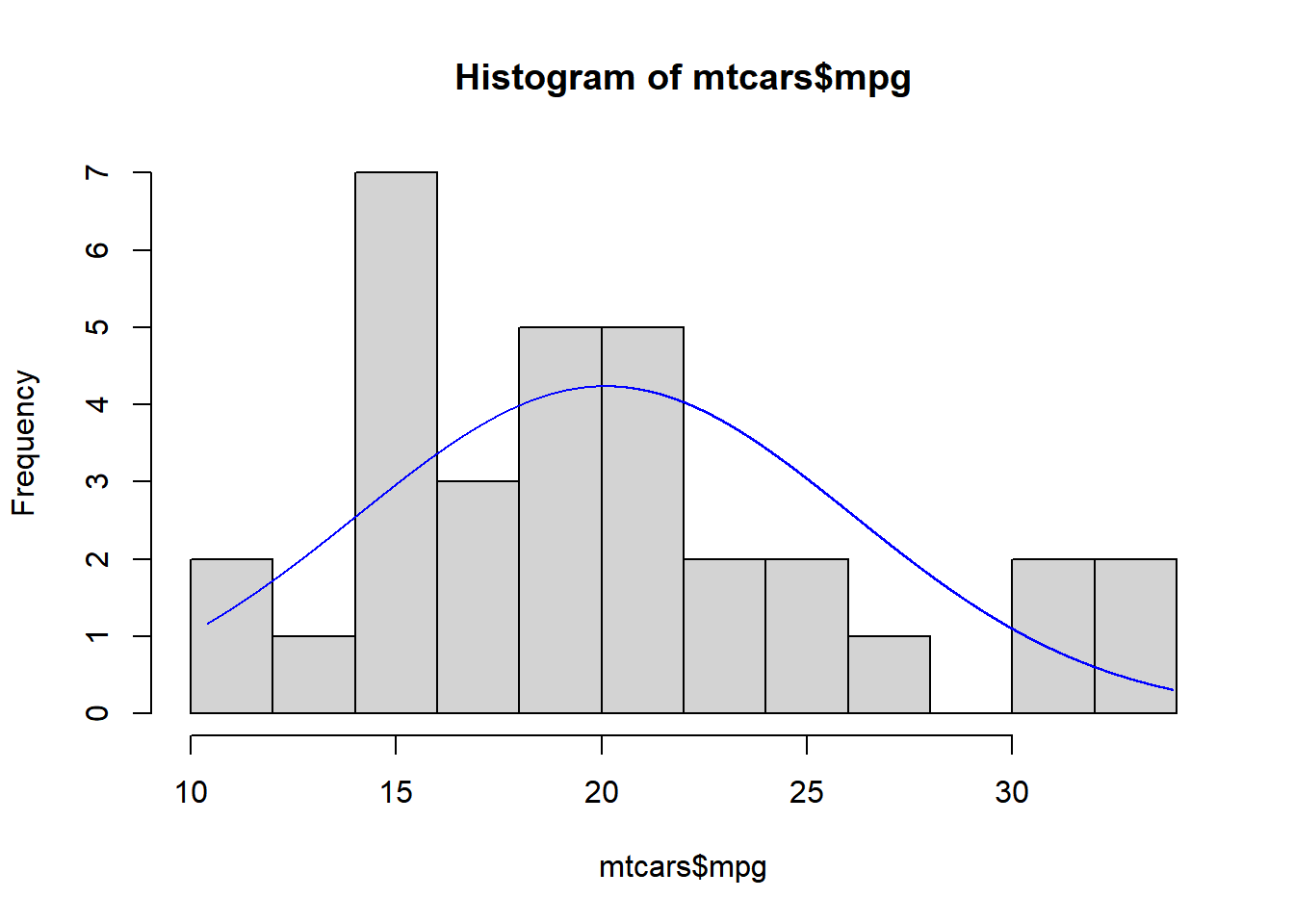
茎叶图(Stem-and-Leaf Plot)
P-P图是累计相对频率的观测值(x轴)与理论值(y轴)的散点图;
Q-Q图是分位数的观测值(x轴)与理论值(y轴)的散点图。
偏度=0 且 超值峰度=0
\[ H_0:总体偏度系数\gamma_1=0 或者总体峰度系数\gamma_2=0 \]
\[ z_i=\frac{g_i-0}{\sigma_{g_i}} \ \ \ \ 临界值z_{1-\alpha/2} \]
shapiro.test(mtcars$mpg)
#>
#> Shapiro-Wilk normality test
#>
#> data: mtcars$mpg
#> W = 0.94756, p-value = 0.1229x <- rnorm(50)
y <- runif(50)
ks.test(x, y) # perform ks test
#>
#> Exact two-sample Kolmogorov-Smirnov test
#>
#> data: x and y
#> D = 0.42, p-value = 0.000246
#> alternative hypothesis: two-sided
x <- rnorm(50)
y <- rnorm(50)
ks.test(x, y)
#>
#> Exact two-sample Kolmogorov-Smirnov test
#>
#> data: x and y
#> D = 0.18, p-value = 0.3959
#> alternative hypothesis: two-sided当\(n\pi(1-\pi)≥5 且X\sim B(n,\pi)\)时,\(P(a≤X≤b)近似等于X\sim N(n\pi,n\pi(1-\pi))在区间(a-0.5,b+0.5)上的曲线下面积\)。
\[ Z=\frac{x-\mu}{\sigma}=\frac{x-n\pi}{\sqrt{n\pi(1-\pi)}} \]
当\(\lambda≥10 且X\sim P(\lambda)\)时,\(P(a≤X≤b)近似等于X\sim N(\lambda,\lambda)在区间(a-0.5,b+0.5)上的曲线下面积\)。
\[ Z=\frac{x-\mu}{\sigma}=\frac{x-\lambda}{\sqrt{\lambda}} \]